Week01

Universal Turing Machine

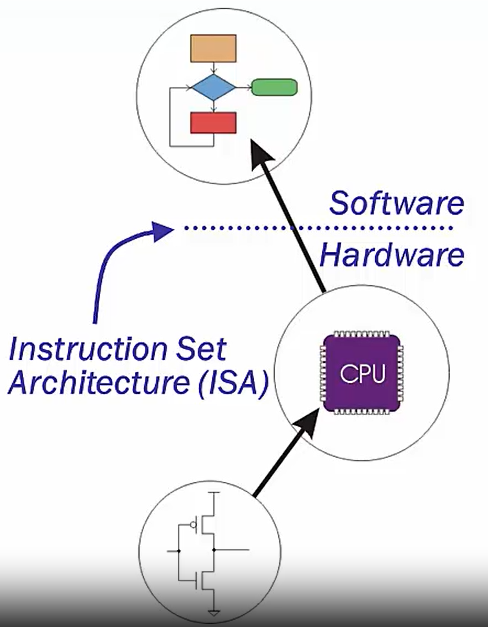
A programmable computer is effectively a Universal Turing Machine (minus infinite memory)

• A “program” describes a computation

• One that can “simulate” any other Turing machine by in putting a description of that machine’s behavior rules

• The behavior is no longer “hard-coded”!

In theory, a computer can compute anything that’s possible to compute…

• Given enough memory and time

Technology

Moore’s law

• Predicted doubling of capacity every 24 months -> Cost halves every two years.

• Has generally held true

Processor

• Executes applicationsthat have been brokendown into sequencesof simple instructions

• Use digital logic circuits, made up of transistors

Abstraction

hardware/software

ISA is the boundary

hardware: ISA, Microarchitecture，Logic Circuits，Devices

software：Problem Statement，Algorithm，Program

Layers

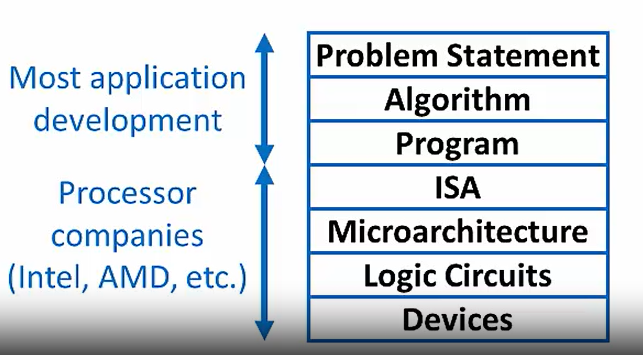
越在上层越抽象 more higher layer more abstraction

Problem Statement

• natural language

• ambiguous，imprecise

—— Software Design: Choose algorithms&data structures tosolve the problem

Algorithm

• step-by-step procedure，guaranteed to finishi

• Definiteness, effective computability, finiteness

—– Programming: Use a programming language to implement design

Program

• Express the algorithm using a computer language

• High-level language, low-level language

区分不同level看hardware还是software

low-level language: assembler, based on ISA

high-level language: complier, based on PS

—– Compilation: Use a compiler to convert the program to machine instructions

---

ISA

• Specifies the set of instructions the computer can perform

• Data types, addressing modes

—– Processor Design: Choose high-level organization and structures to implement ISA

Microarchitecture

• Detailed organization of a processor implementation

• Different implementations of a single ISA

—– Logic/Circuit Design: Choose gates and other low-level structures to implement components

Logic Circuits

• Combine basic operations to realize microarchitecture

• Many different ways to implement a single function(e.g., addition)

—– Implement & Fabricate: Transform logic circuits into masks for transistors and other layers, then fabricate

Devices

• Transistor-based implementation of logic circuits

• Chip layout masks

• Properties of materials, manufacturability

Abstraction to Manage Complexity

higher level of abstraction = more abstract

Electrical Information

Almost all computing systems are digital

Analog：Continuous range of values

Digital：Discrete set of values （more abstract）

Digital is an Abstraction of Analog

Binary Information
Any data processed by a digital computer is represented by sequences of 1s and Os

Week02

Positional Notation

Digits represent powers of the base(radix)
Each digit D in radix r is restricted to $0≤D< r$

N-digit non-negative integer with radix r:
$D_{N-1}….D_1D_0= D_{N-1}×r^{N-1} + …+ D_1×r^1 + D_0×r^0$

Binary (Base 2) Octal (Base 8) Hexadecimal (Base 16)

Each position represents a power of base

Digit value says how many of that power of base

Value vs. Number

A value is a particular quantity

A number is a way to represent a value

To know the value indicated by a number, you need to know the format!

The contribution of each digit to a number’s value is determined by its position and the base

Conversion

Decimal to others: divide by base, the remainders are the digits

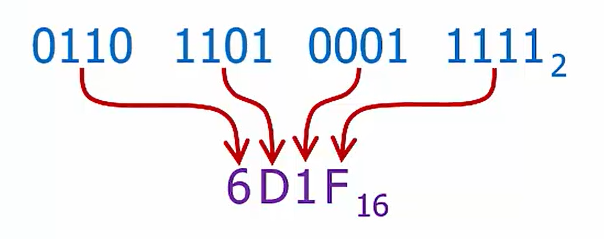
Binary to Hex: Directly substitute a hex digit fora 4-bit binary number (or vice versa!)

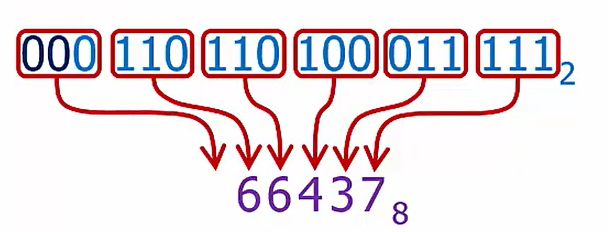
Binary to Octal: Directly substitute a hex digit fora 3-bit binary number (or vice versa!)

Octal to Hex:

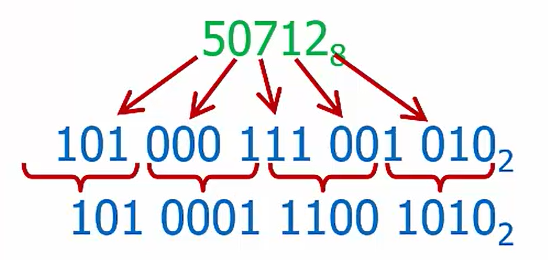
Use binary as an intermediate form!

Decimal to Octal, Decimal to Hex: use Binary as an intermediate form

left: most significant, right: less significant

Multiply: move to left, Multiplying a base $R$ number by $R^N$ “shifts” the number left by $N$ positions

Divide: move to right, Dividing a base $R$ number by $R^N$ “shifts” the number right by $N$ positions

Signed Number

In decimal, we show a number’s sign using asymbol (+ or -) in front of its magnitude Hence the name “signed-magnitude”…

2’s-Complement Representation

Positive numbers start with 0

The rest of the bits work the same as unsigned binary

Negative numbers start with 1

The interpretation is more complex

十进制负数 到 二补数：-5 到 5 -> 0101 -> 1010 + 1 = 1011

二补数负数 到 十进制负数1101 -> 0010 + 1= 0011 -> 3 -> -3

Addition

Addition works the way it does for unsigned binary numbers

Subtraction

Instead of subtraction with borrowing, we add the negation of the value we wish to subtract

This method simplifies computer hardware

Operand/Result Bitwidths Match

Operands and results must have the same number of bits for the math to work correctly

operand是符号两边的数字

Signed Extension

前面是0就补0，是1就补1

每种表达的范围，超出范围就overflow

unsigned number: $[0,2^{n}-1]$

signed number: $ [-(2^{n-1}-1),2^{n-1}-1 ]$

2’s-complement number: $[-2^{n-1},2^{n-1}-1]$

最小的数为1+n-1个0，最大是0+n-1个1，$[1000,0111]$

Overflow

不管哪种方式，只要大于以上表达数的范围就overflow，表现为显示答案错误，sign错误

The result cannot be correctly represented in the required number of bits.

lf adding two negative 2’s-complement numbers overflows, the sign of the result will appear to be non-negative.

1101 -3 |1001 -7

1100 -4 |1100 -4

————————

1001 -7 |0101 5 overflow

lf the result of adding two positive 2’s-complement numbers appears to be positive, then the operation did not overflow.

lf adding two unsigned numbers overflows , the result will appear to be
smaller than it should be.

Week03

Fixed Floating

When the format defines a “fixed” position for the radix point within the number’s digits, it is called fixed-point

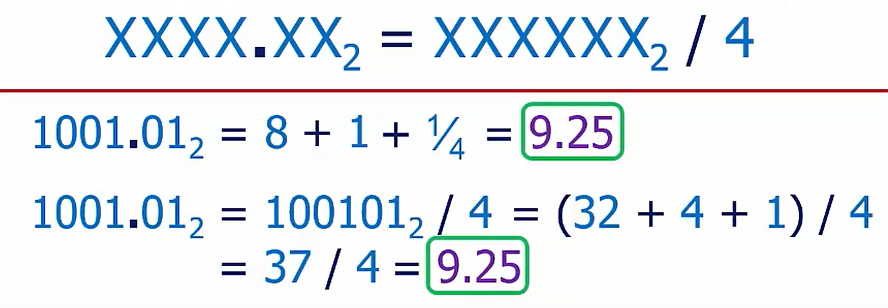
Floating-Point

Floating-point: the format defines a way to encode the radix point location into the number(i.e., the position is not “fixed” in one place)

• More flexibility than fixed-point… and more complexity!

• Scientific Notation is floating-point

IEEE 32-Bit Floating-Point

$(-1)^{sign} 1.signficand 2 ^{exponent-127}$

Format Comparison

Range: from the leftmost to the rightmostrepresentable values on the number line

Precision: number of significant digits

Integer: $XXXX XXXX$

• precision: 8 bits

• range: $[0,2^8-1]$

Fixed: $XXXX.XXXX$

• precision: 8 bits

• range: $[0,2^4-1+ 1- 2^{-4}]$

Float: $1.XXXX * 2^{XXXX}$

• precision: 5 bits notes（不需要转成十进制） precision=1+significand

• range: $[1,(1+1-2^{-4} )* 2^{2^4-1}]$

A 32-bit IEEE floating-point number has greater range and lesser precision compared to a 32-bit 2’s-complement integer.

ASCII

A computer stores text in memory as binary

It uses 8 binary-bits, 2 hex-bits (has been extended) to represent 128 different characters

Alphanumeric characters A-Z, a-z,0-9, encoded to allow easy sorting and transformation

Week04

Logic Functions

Ones and Zeros

• Digital circuits manipulate voltage levels that weconsider more abstractly to be ones and zeros

• We call these circuits logic circuits because they operate on and produce Boolean results

• Boolean variables have only two possible values
  TRUE (corresponding to “one”)
  FALSE (corresponding to “zero”)

Logic Operator

AND: $A \cdot B$

OR: $A + B$

NOT: $\bar{A}$

XOR: $A \oplus B$ 相同是0，不同是1

The Odd Function

ex:$(A \oplus B) \oplus C$

output is 1 only when an odd # of the inputs are 1

Bitwise Logic Functions

A bitwise operation computes each bit of an N-bit result based on the value(s) in the
corresponding position of the N-bit operand(s) 按位运算

Combinational Logic

we think of logic circuits as having Boolean input values and producing Boolean results
In reality, they are built from transistors that connecteach output to power or ground based on the design of the circuit and the voltage level of each input

• Logic circuits are at a higher level of abstraction

• Each transistor acts like a switch…

Transistors

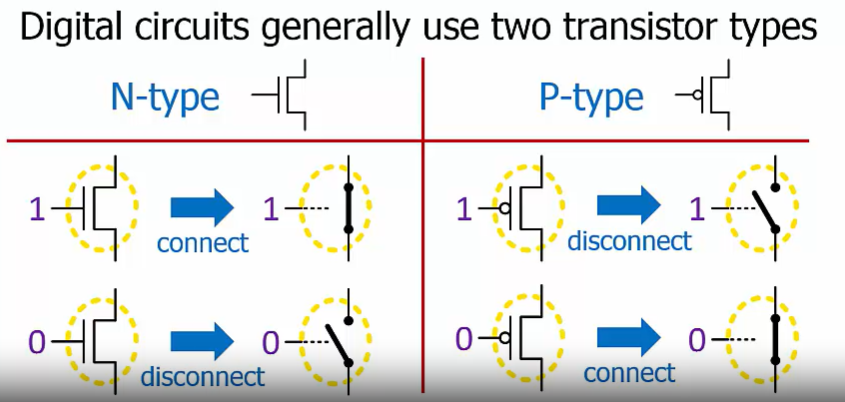
A logic gate is an electric circuit that contains transistors that connect the output to power or ground based on the input voltage(s)

• power -> voltage interpreted as logic 1

• ground -> voltage interpreted as loaic 0

  NOT gate use 2 transistors

Logic Gates

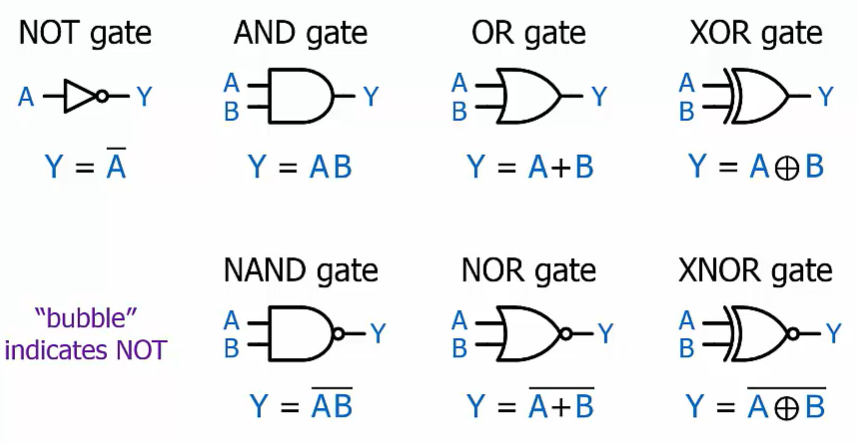
The shape of the gate allows us to visually determine all of these.

The inputs of these gates don’t need to be labeled because in these functions, the order of inputs doesn’t matter.

Combinational Blocks

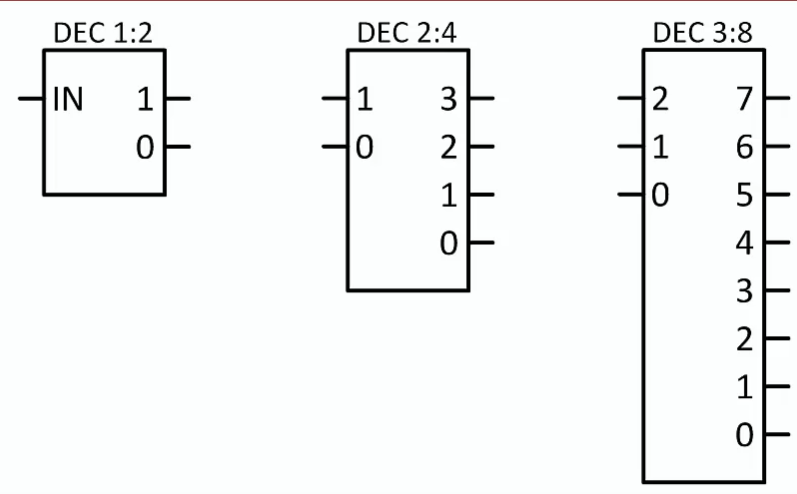
Decoder

Converts an n-bit input codeword into a unique m-bit output value, where $m=2^n$

Exactly one output can be true at any given time

Here we are only concerned with how the decoder behaves, not how it is constructed internally

If the input value is N, the output is N

When we represent a logic structure with a block, the internal details are hidden. When using the block in a logic circuit, we only need to know what the block does.

Inside the block’s symbol, we label each pin to indicate the pin’s function in the underlying logic structure.

When we draw signal names or Boolean values on the outside of the block near the pins, they indicate what is externally connected to the block (the Boolean value or signal name.

We label each decoder output with a decimal number that is equal to the input code value that causes that output to be 1.

A decoder indicates what number is present at the decoder’s input(s) by making the decoder output pin labeled with the same number output the value 1.

Multiplexers(Muxes)

Selection: based on the select input(s), choose one of the data inputs to drive the output

• Output is equal to one of the data inputs

• Select inputs indicate which data input

n select lines, $2^n$ input lines

The output of a multiplexer always has the same value as one of its data inputs.

The multiplexer’s select inputs control which of its data inputs is sent to the output.

A multiplexer chooses between multiple signals by outputting the data inputlabeled with the same number as current value of select input(s).

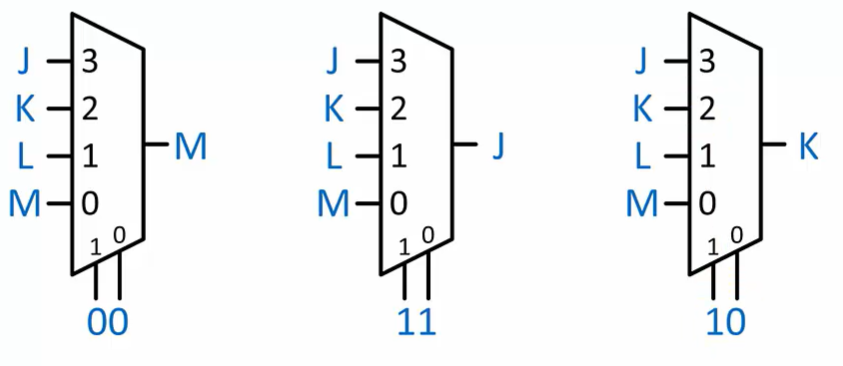
Data inputs must be labeled to indicate which input is chosen for a given select value
Select inputs must be labeled so we know the ordering of bits within the select value We need to interpret the select as a binary number

Exception: a 2:1 mux has only one select signal so it does not need a label

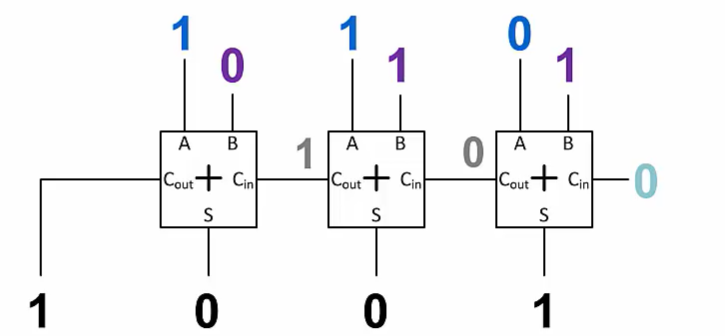
Adders

Full adder:

A structure that performs the addition for one bit position of a multi-bit binary addition operation.

Accept three inputs: a bit from each addend and a carry value from bit position to the right
Produce two outputs: the sum bit at that position, and a carry value to send to the bit position to the left

A full adder performs addition for a single bit position

Cout,Cin: 进位

Ripple Carry Adder

A series of full adders, where each full adder performs the addition for a single bit position.

Week05

Combinational Logic

So far, all of the logic circuits we have talked about have been combinational

• Circuit outputs only depend on current input values

• Adder, Mux, Decoder,

Sequential Circuits

The behavior of a sequential logic circuit is determined by both its current and past input values.

• flip-flop, register, fsm

• Some systems need to store information about past behavior to know how to react to inputs

• Sometimes just need to store data for later access

• Logic circuits whose outputs depend at least in part on past input behavior.

A circuit’s current state is the binary number that is currently stored in the circuit’s flip-flops.

The state of a sequential logic circuit can change, only at the triggering (active) edge of its clock signal.

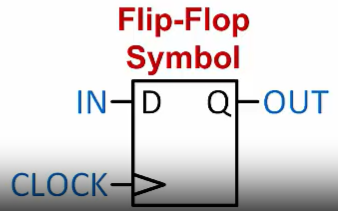
Flip-Flop

It has one bit of data input, one bit of data output
It also has a “clock” input that controls when the value carried by the input signal is stored into the flip-flop

The value held by a flip-flop cannot change until the clock allows it(or power is lost to the system…)

The flip-flop’s output is always equal to the value it is storing

Clock signal

A clock is a special signal that oscillates between 1and 0 at a specific frequency

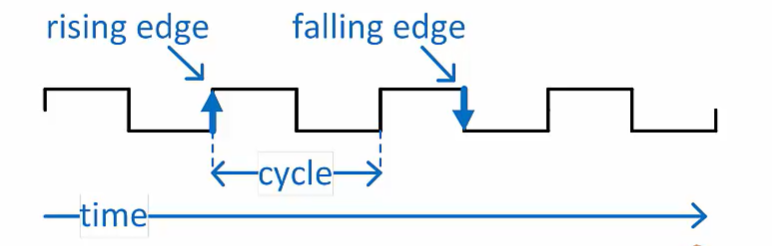
This D flip-flop updates when the clock transitions from 0 to 1(rising edge)

The flip-flop input is only stored at the rising clock edge(“triggering” edge)

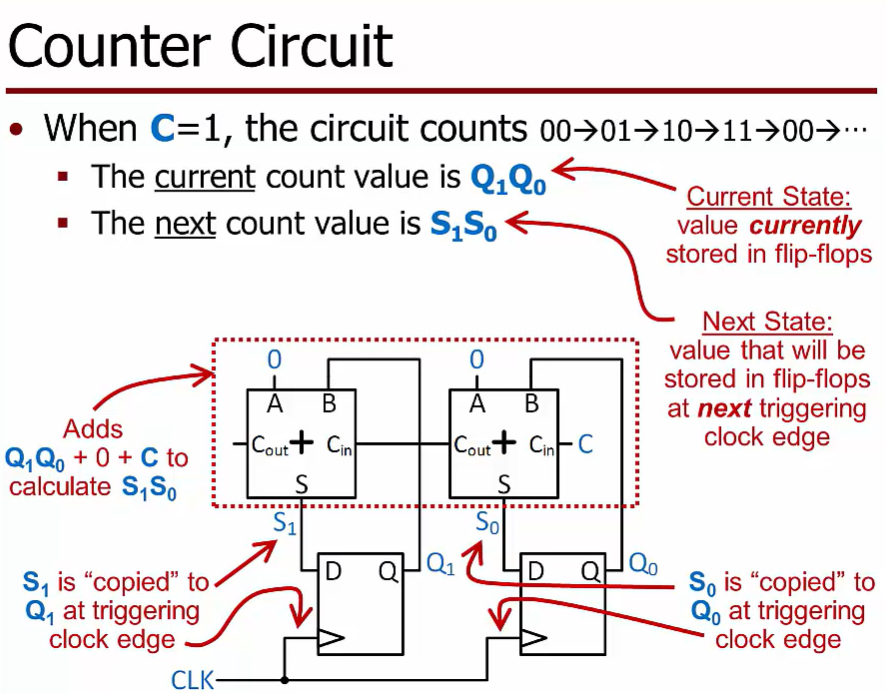
Counter Circuit

约等于每次给自己加1

Finite State Machine

Any practical sequential circuit is a Finite State Machine (FSM)

State: current “status” -> the contents of the flip-flops

• state diagram of a Flip-Flop only 2 state

• counter state diagram only 4 state

Each state in an FSM is assigned a binary code

• The FSM contains one flip-flop per bit of state

• During operation, the code stored in the FSM’s flip-flops tells us (and the machine) which is the current state.

• The next state becomes the current state when the flip-flop contents are updated

The FSM’s behavior depends both upon the current state and the input(s)

• The next state is a function of the current state and current input values

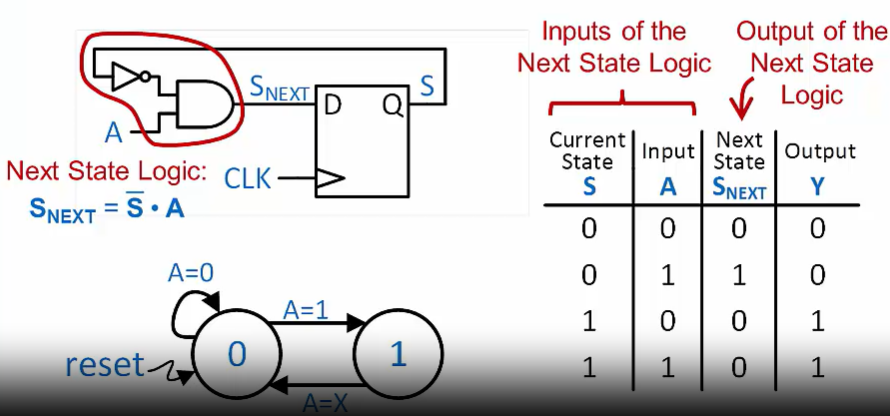
A state diagram describes the behavior of a state machine by showing for each state, what it should do in response to the inputs.

A given row of the state table lists the output value(s) it will produce for that row’s current state.

Hardware Design

A register is a group of flip-flops used to storemulti-bit binary values

Register Memory

Register

A register is a group of flip-flops used to store multi-bit binary values

Counter

Use adders and registers

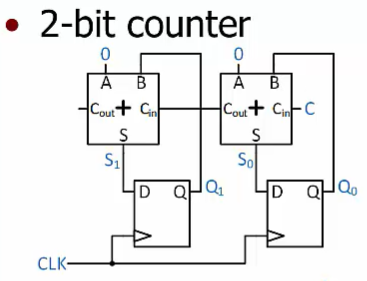
Enable

Sometimes we want a flip-flop to “hold” its value for multiple clock cycles, regardless of its input

• But a flip-flop always stores the input value at the triggering edge of the clock…

Solution: add logic so that we can choose to store a new value or the value already in the flip-flop

• Selection based on the value of a special input signal called an enable

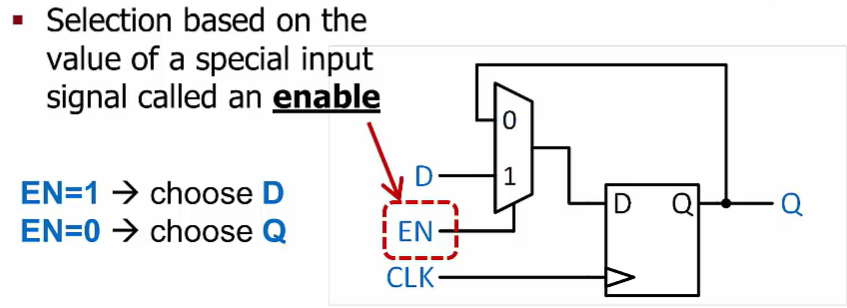
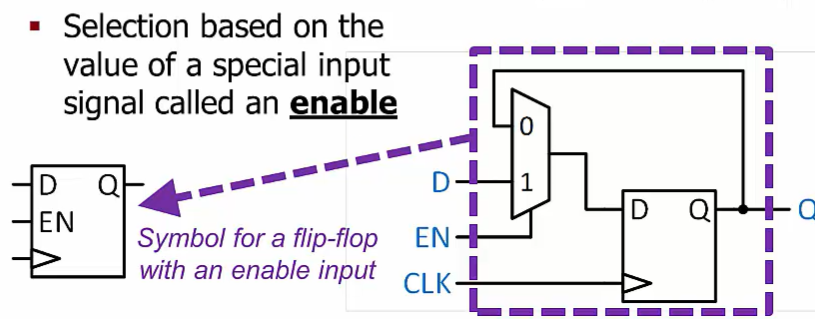
If we want to hold a value for longer, we can add a set of multiplexers full adders AND gates to choose between an external input value and the current register value.

The register’s clock enable signal selects which of those values will be stored into the register at the next triggering clock edge.

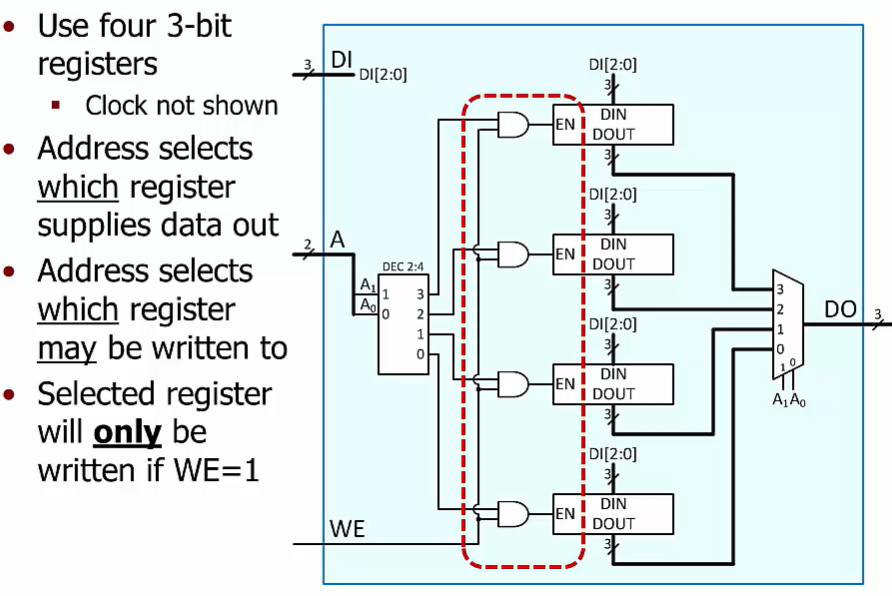
Memory

$M$-bits number specifies $2^M$ locations

Each location stores a single N-bit word

$N$ is the data size of the memory

The capacity of a memory is: $2^M * N$

A memory is conceptually like an array of registers

The capacity of a memory is equal to the total number of registers it contains.

Only one location can be accessed at a time,either to write (store) a value or read a value

To access a register, we index into the array using the address for that register

set WE to 1 for write, WE to 1 for read

In a memory :

• $n$-bits address for $2^n$ locatioins

• the number of address bits dictates the maximum number of addressable locations in the memory

Address selects which register supplies data out using muxs

Address selects which register using decoders

The data word size (# bits per data word) of a memory dictates 1.The number of data input and data output pins that the memory must have. 2. The number of single-bit storage elements required per memory location.

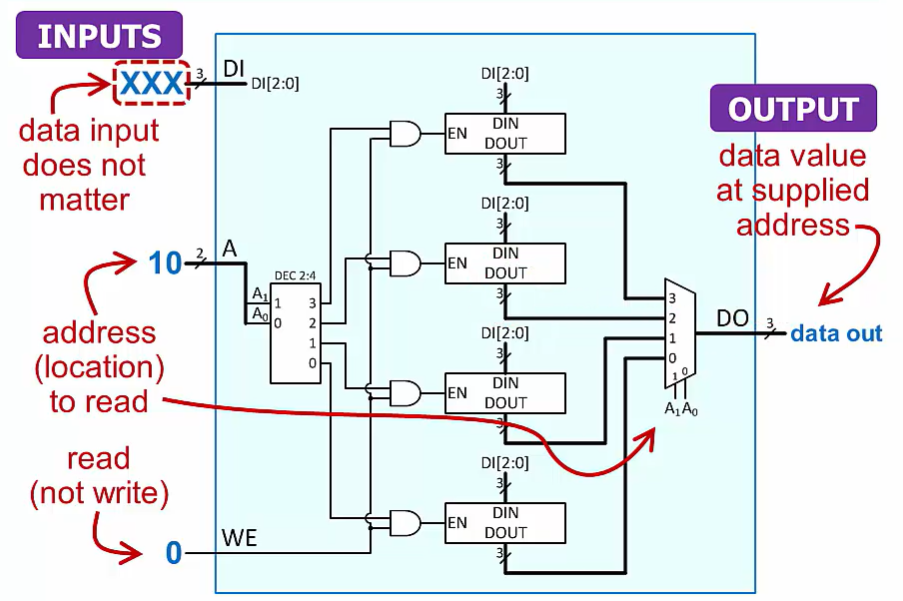
Read

using mux to select output location from read

no inputs and we

Write

input data, using decoder to select address to write, we enable

no mux and output

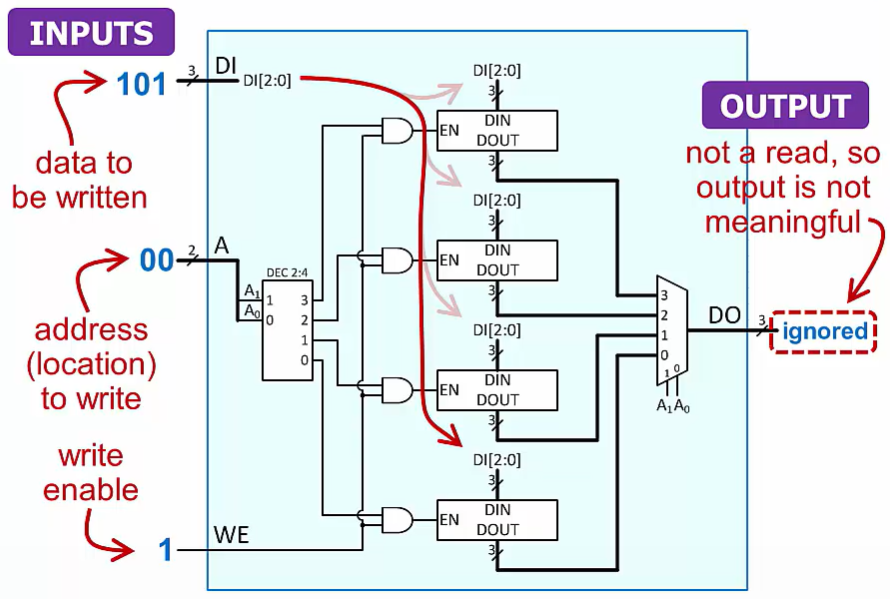
读进去mux SD1 SA1 SD2 SA2，对应的 bit也是对应

写入DA 地址，DD data 进入decoder

Week06

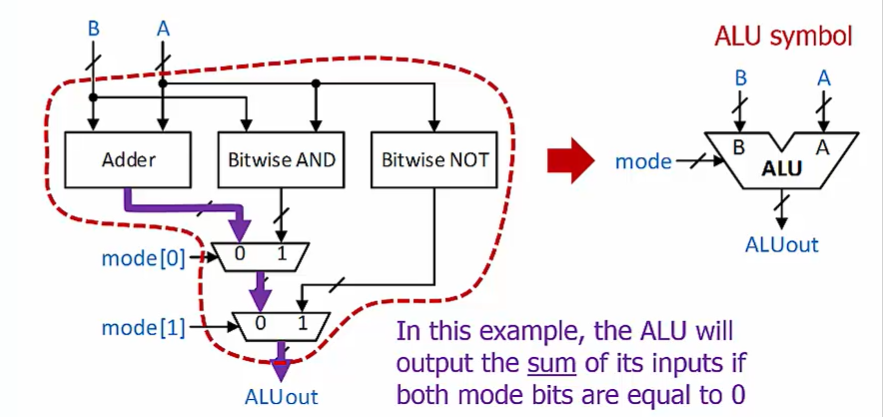
ALU(The Arithmetic Logic Unit)

A set of logic structures that perform a set of different possible computations on the inputs.

One or more arithmetic operations (e.g., add, subtract).

One or more logic operations (e.g.,AND,OR,NOT)

Includes a set of multiplexers that, based on a set of control signals, choose which result to send to the ALU output

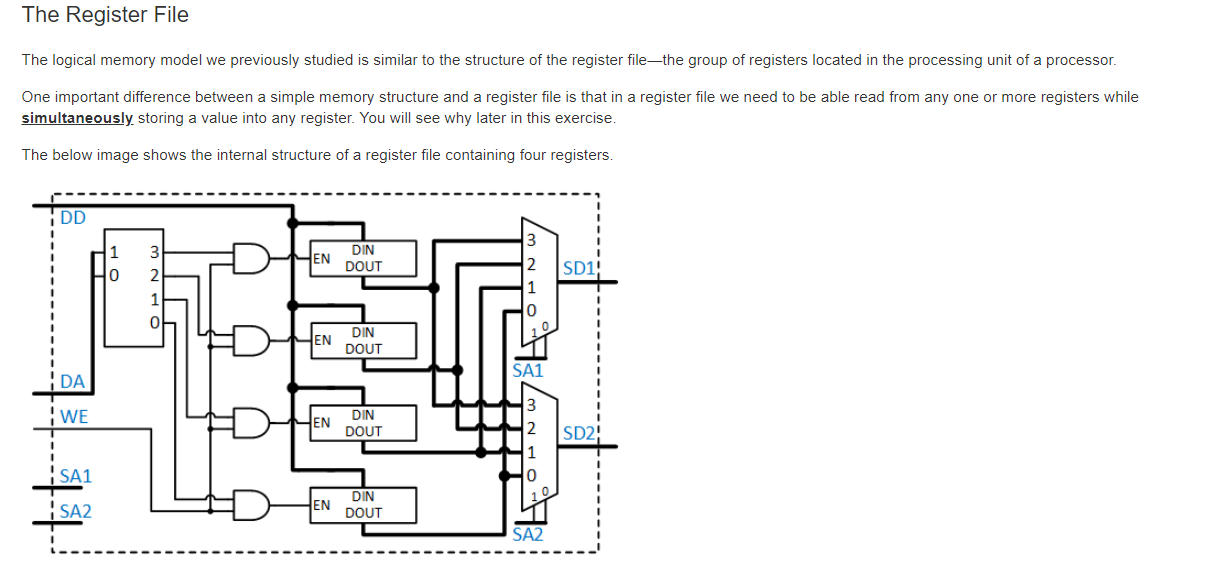
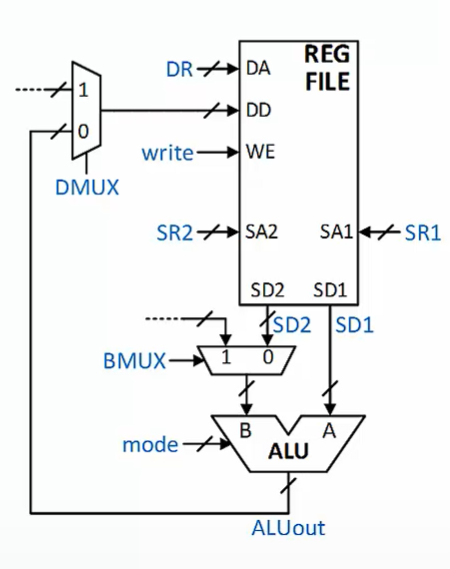
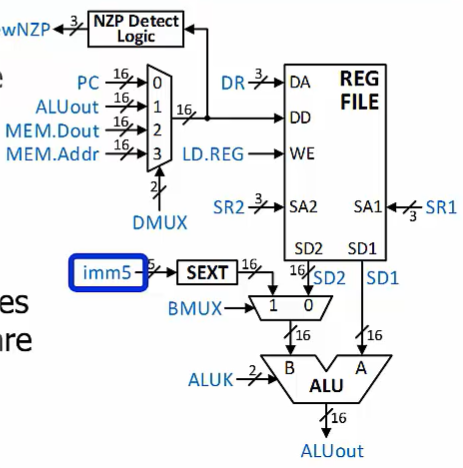
The Register File

DA data address, DD data

A register file is asmall memory located near the ALU

Read from multiple locations and write toone location

Address inputs control which registers are accessed

Write enable controls whether the destinationinput is stored or not

In the register file, the decoder structure chooses which register is written to, and the multiplexer structures choose which registers are read from.

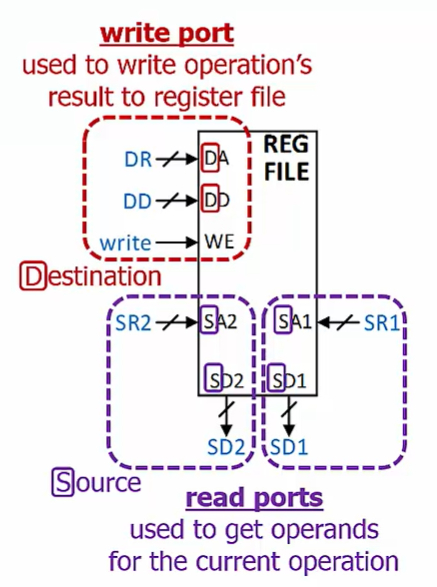
The Processing Unit

Contains the ALU and the register file

Control signals dictate which operation is performed on which data and where the result is stored

A program is a sequence of instructions, each of which describes one “step” of the program

One computer processes one instruction at a time

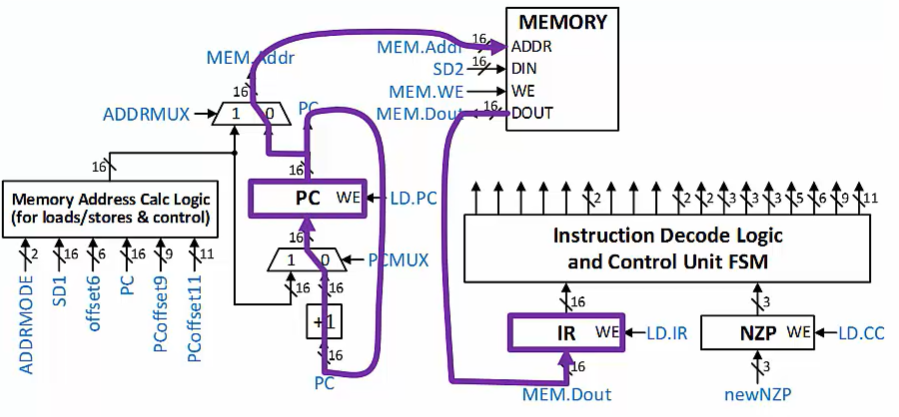
Control Unit

Fetches instructions one by one from memory

Tells each part of the computer what to do to execute each instruction

• It tells the processing unit and the memory what to do in response to each instruction

• It keeps track of which instruction in the program should be fetched next

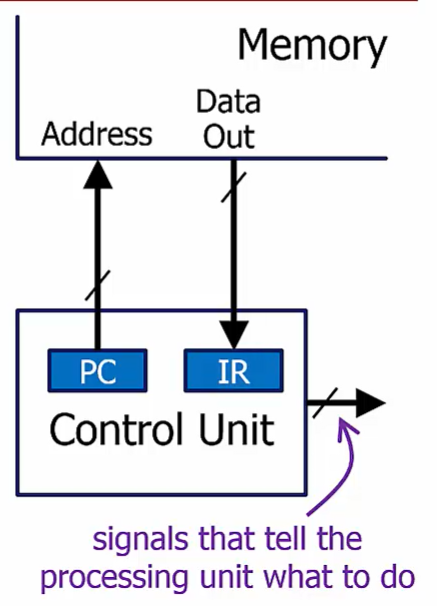
Contains two specialregisters:

Program Counter (PC): contains the address of the next instruction

Instruction Register (IR): contains the current instruction

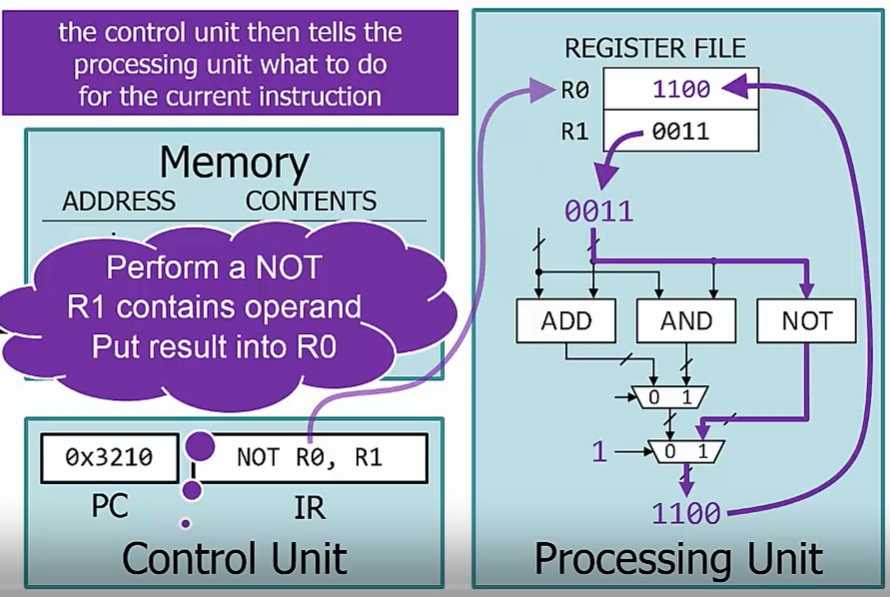
von Neumann Compute Model

In the von Neumann compute model, instructions and data are stored in memory

Another key feature of the von Neumann model is the fact that instructions are executed one at a time

In a computer, an instruction consists of two parts, the opcode, which specifies what the instruction does, and the operand(s), which specify the data it operates on.

Instructions are encoded as binary values and stored in the computer’s memory

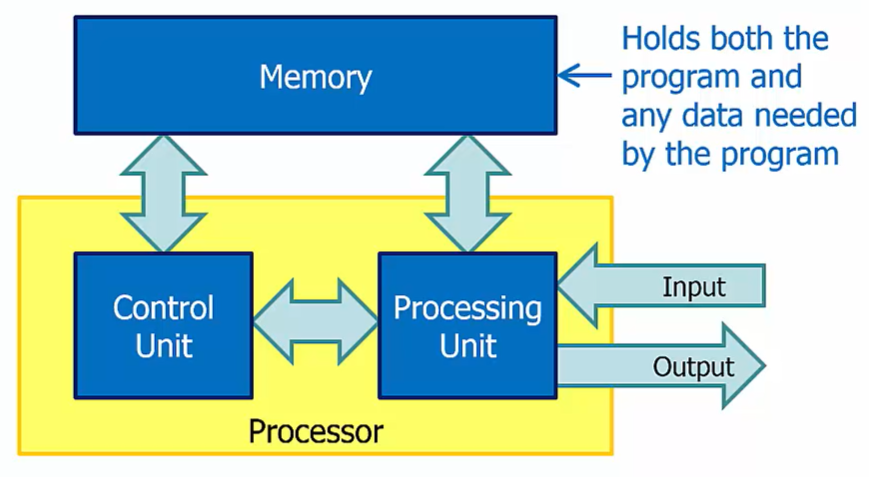
Instructions

Instructions are divided up into fields (groups ofbits), each providing into about the instruction.

A program is a sequence of instructions

The fields and their sizes are also dictated by the ISA

Opcode: indicates the operation type (ADD, JMP, etc).

Other bits indicate operands and other information

Instructions from other ISAs will look different· Different number of bits, different fields, etc.

In a stored-program computer, the instructions that make up a program are stored in memory. This means that

By storing different sequences of instructions in memory, we can make the computer do different things.

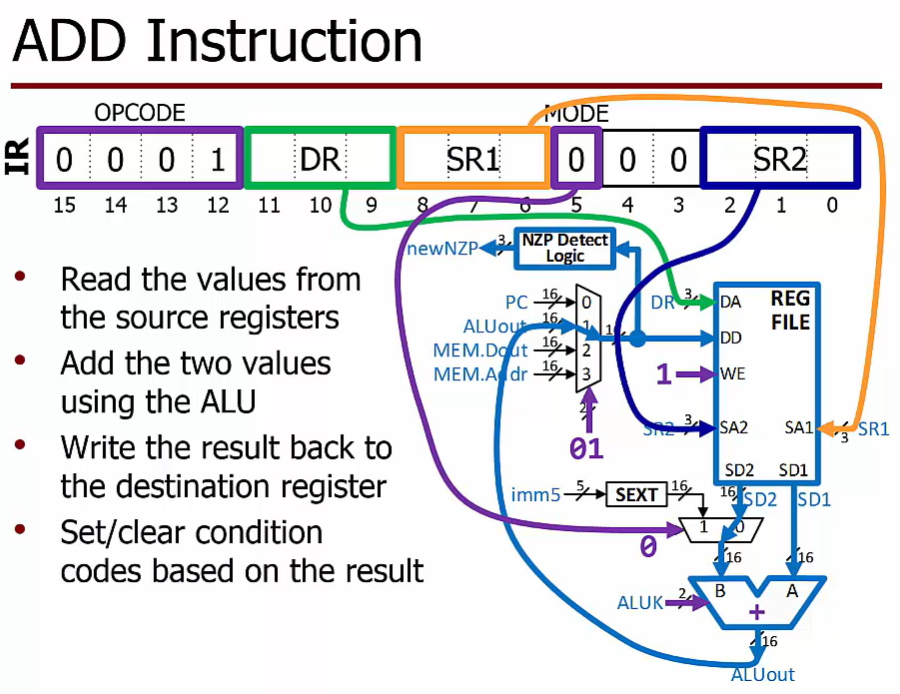
Five fields: opcode, destination register, source register 1, mode, source register 2
Each field represents a separate piece of information about the instruction

Operate Instructions

Use the ALU to perform a computation
Operands include value(s) in register file and possibly a constant encoded in the instruction

ex : R3 <- R4 +R7

R0 <- R0 +1

Data Movement Instructions

Copy data between the memory and register file

Allows processing of more data than can fit in theregister file (which is often relatively small)

• Load - copy from memory to the register file

• Store - copy from the register file to memory

ex: R1 <- mem[R5 + 2] : read from memory using an address 2 greater than contents of R5,and put the result into R1

Control Instructions

Change the sequence of execution by changing the value in the Program Counter (PC)

• Loops: need to execute instructions more than once

• If/else conditions: need to skip certain instructions.

• Subroutines (similar to functions or methods in C/Java)

ex : PC <- R6 : overwrite the PC with the value in register R6

Instructions Cycle

Describe the different phases of execution of each instruction
Not all phases required for every type of instruction

Repeat forever
The control unit performs different tasksin each phase

It is a fsm

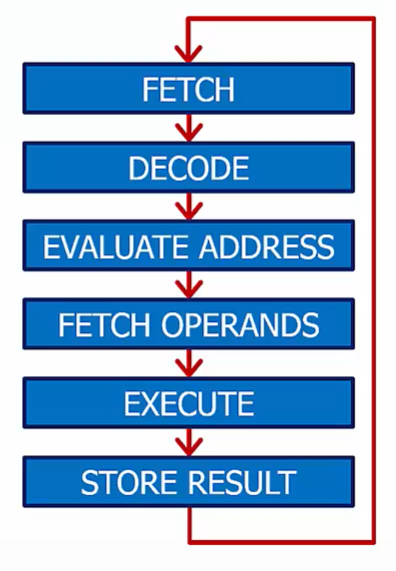
Fetch: The next instruction is read from memory

Decode: The control unit determines what the components of the processor should do based on the value in the instruction register (IR)

Evaluate Address: If a memory operation is needed, the address for it is calculated

Fetch Operands: One or more operands that are needed for an operation described by the instruction are read from memory or from the register file

Execute: Performs the “work” described by the instruction

Store Result: The result of the operation is written to the destination register indicated by the instruction

Fetch

• Read an instruction from memory

Address of the instruction contained in the PC

• Put value read from memory into the IR

The binary value that represents the instruction

• Increment the PC to”point” to the next instruction in memory(the next memory address)

Decode

Determine what the instruction says the processor should do

The instruction type is indicated by the opcode

Identify operands for the instruction based on the bit values in the
instruction’s fields

FETCH and DECODE are needed for all

Operate

fetch operands, execute, store result

Get the operands

• Read from register file using source reg. address(es) encoded in the instruction

• If instruction uses a constant, extract its value from the instruction

Perform the ALU operation

Write to the register file.

• Use destination reg. address encoded in instruction

• Use data produced by ALU

Data Move (Load)

evaluate address, fetch operands, store result

Calculate the memory address that will be used to read from memory.

• May involve register read and/or extracting a constan

Read from memory

• Use address calculated in EVALUATE ADDRESS phase

Write to the register file.

• Use destination reg. address encoded in the instruction

• Use data value returnedfrom memory

Data Move (Store)

evaluate address, fetch operands, execute

Calculate the memory address that will be used to write to memory

• May involve register read and/or extracting a constant

Read from the register file.

• Use source register address encoded in the instruction

Write to memory

• Use address calculated in EVALUATE ADDRESS phase.

• Use data value that was read from the register file

Control

evaluate address, execute

Calculate the memory address that will be written to the PC

• This is the address of the next instruction that will be executed

• May involve register readand/or extracting a constant

Determine if the PC shouldbe updated (if conditionalbranch), and if so do it.

• Update if the condition is met or is unconditional jump

Week07

LC-3 Overview

Instructions are 16 bits wide, divided into several fields of information

• Bits 15 through 12 are the 4-bit opcode

• The opcode for the current instruction is in IR[15:12]

• Remaining bits are divided up into various other fields(the exact set of fields depends in part on the opcode)

Processing Unit

Eight general-purpose registers in the register file

• Referenced using a 3-bit register address

• LC-3 assembly language:

• R3 is register w/address 011

• Data word size is 16 bits

Constant (immediate) values encoded into instructions are 2’s-complement format

• sign-extended to 16 bits before processing

Control Unit

Control Unit coordinates and controls processor resources to execute a program

Fetch

Read from memory using PC as address
Place value read from memory (the next instruction that will be executed) into the IR
Increment the PC

Control Signal

Finite State Machine and instruction decode logic generates signals to control other resources
Affected by the binary instruction in the IR

If current instruction is a conditional Control instructional output is also affected by condition codes (CCS)

• Change the PC only if the condition(s) indicated in the current instruction is/are true

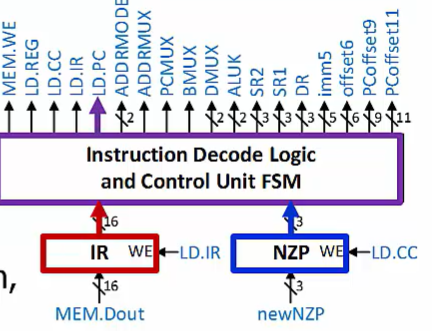
Condition codes (CCs) are stored in a special register

Indicate information about the most recent result in the Processing Unit
Negative, Zero, or Positive

Three 1-bit flags; exactly one of these equals 1 at any time!

Control Unit causes CCs to update as part of executing some instruction types

• Operate instructions

• Load instructions

Memory Address Calculation

Other logic calculates memory addresses.

Addresses used for Data Movement (loads/stores)

New PC value for Control instructions

• Remember - the PC holds a memory address….
• These calculations are specified by the ISA

The address calculation method depends on the memory addressing mode of the instruction

• Add an offset to a value from the register file

• Add one of two possible offsets to the PC

Offset values are decoded from the instruction

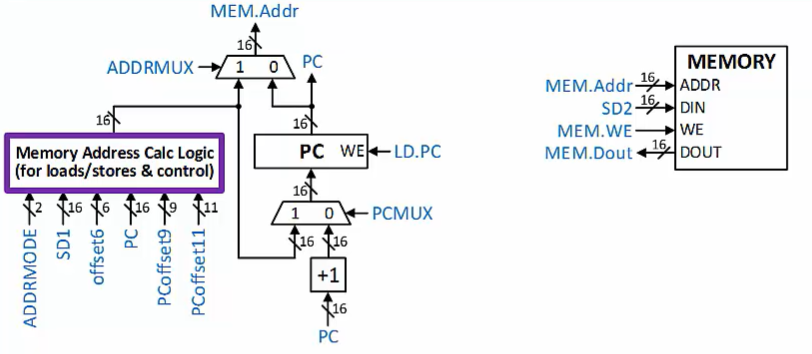
Memory

Holds both instructions and program data

• Memory’s DOUT (data out) output goes to both the IR in the Control Unit and to the Processing Unit

Only Data Movement store instructions write to memory
Memory’s DIN(data in) input comes from the Register File

16-bit memory addresses(range: 0x0000-0xFFFF)

16-bit memory data word size

• Same as size of instruction and register data word size

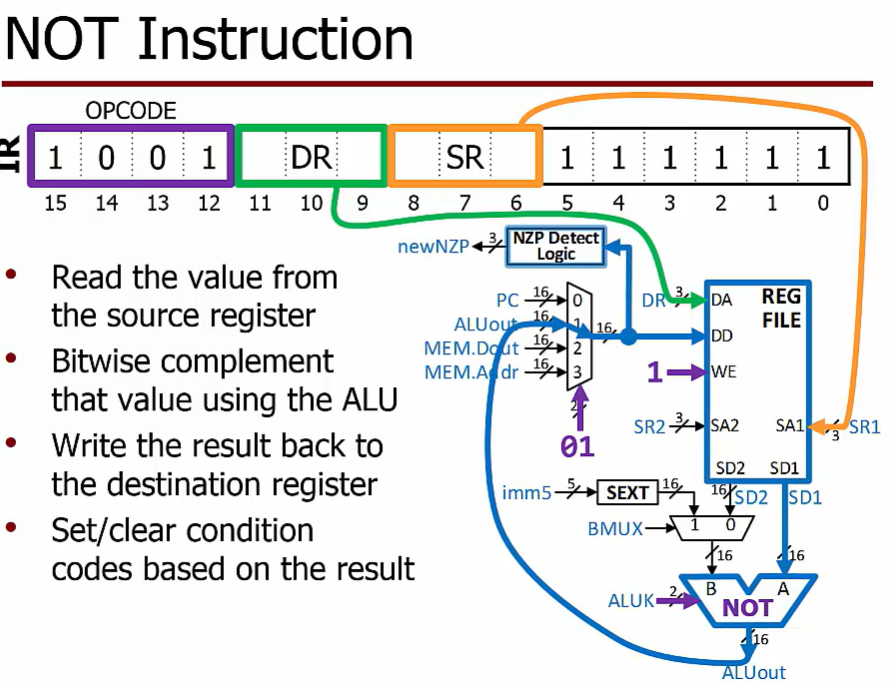
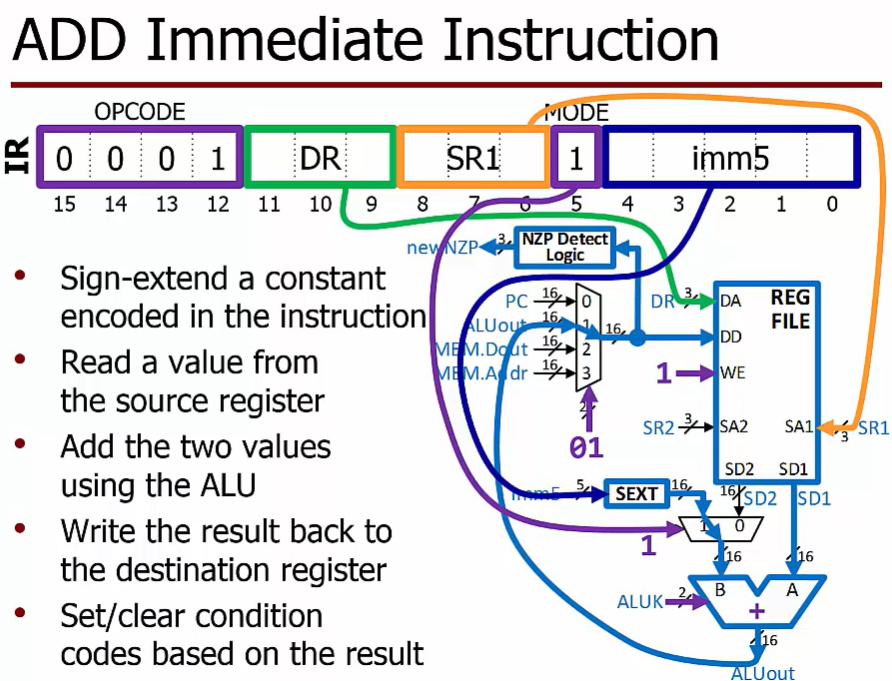
Operate Instruction

Perform computations using the Processing Unit

At least one source operand is read from the register file

May have $2^{nd}$ operand

Another register value

A constant encoded into the instruction itself

Performs an ALU operation

Writes the result back to the destination register in the register file

Sets/clears condition codes based on the result

NOT

R register A address D data

D写入目标 S输入

ADD

ADD Immediate

AND

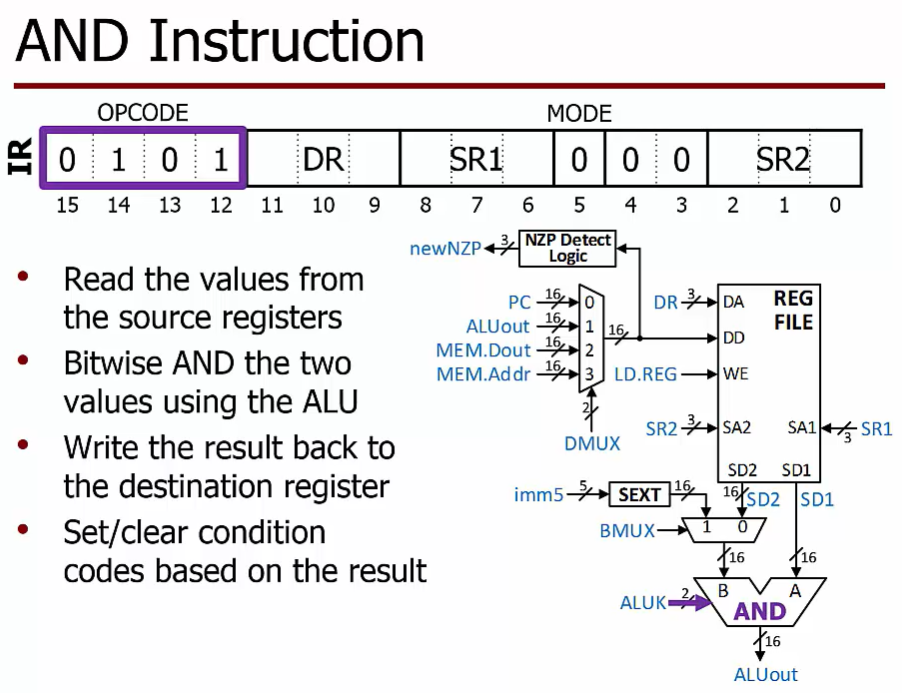
AND Immediate

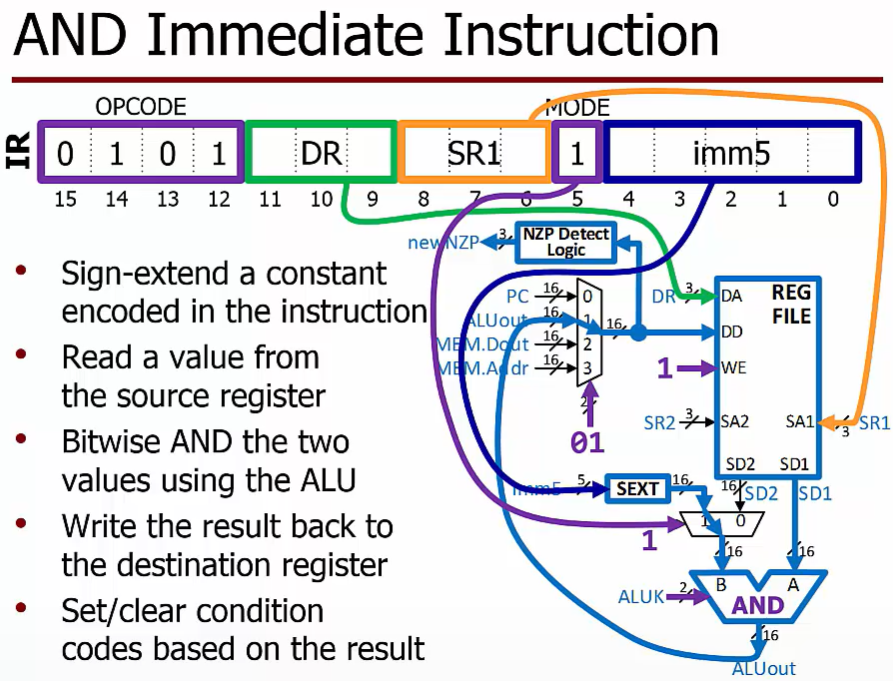
The 5-bit imm5 value (which comes from IR[4:0]) is sign-extended before being sent to the ALU.

How does the value of the SEXT logic’s output relate to the value of its input?

The output value is equal to the input value, but expressed with a different number of bits.

Simple Assembly Programming

Most people do not want to program in binary machine language…
Assembly language is close to machine language (still specify each instruction), but it has several features that make it easier to use

• Opcode mnemonics, comments, labels, symbols, etc…

The assembler translates assembly language programs into machine language that can be executed by the processor

• Performs low-level computations for the programmer.
• Creates an object file containing binary program instructions and other information

.ORIG started memory address

.END end of program

Initialization

赋值$R1$为$x$，Only works for values in range [-16,15] because the immediate is a sign-extended 5-bit number (imm5)

AND R1, R1, #X

Register Copy

ADD R1, R2, #0 ;R1 <- r2 and r1, r2, #-1 ; 0xffff 

Increment or Decrement

The ‘#’ symbol indicates that the number is given in decimal; ‘x’ indicates hex, ‘b’ indicates binary. Can represent 1210 as #12, xC, or b1100
If you want to use the minus sign, use decimal

ADD R7, R7, #1 ; R7=R7+1
ADD R6, R6, #-1 ; R6=R6-1

Negation and Subtraction

NOT R6, R6
ADD R6, R6, #1  ;negate R6

NOT R0, R4
ADD R0, R0, #1 R0 <- -r4 add r0, r3 ; r0 <- r3-r4 

Masking

determine if a number is odd or even

AND R5, R5, #1 ; 1 means odd, 0 means even

# R2 <- 1 2*r0-r1 add r0, r0 not r1, r1 r2, 

Week08

Basic Data Movement

Similar to a variable in high-level languages

Assembler directives reserve space in memory and give them names that we can use to refer to addresses in our assembly-language program.

• The assembler converts these labels to the addresses the processor needs (…actually, a way to calculate them…)

The purpose of a load instruction is to copy a data word from memory to the register file. From the processor’s point of view, it loads a value from memory.

To execute a load or store instruction, the processor must calculate the memory address of the location to be accessed, which is called the effective address.

The method by which the address is calculated for a specific instruction is referred to as the addressing mode.

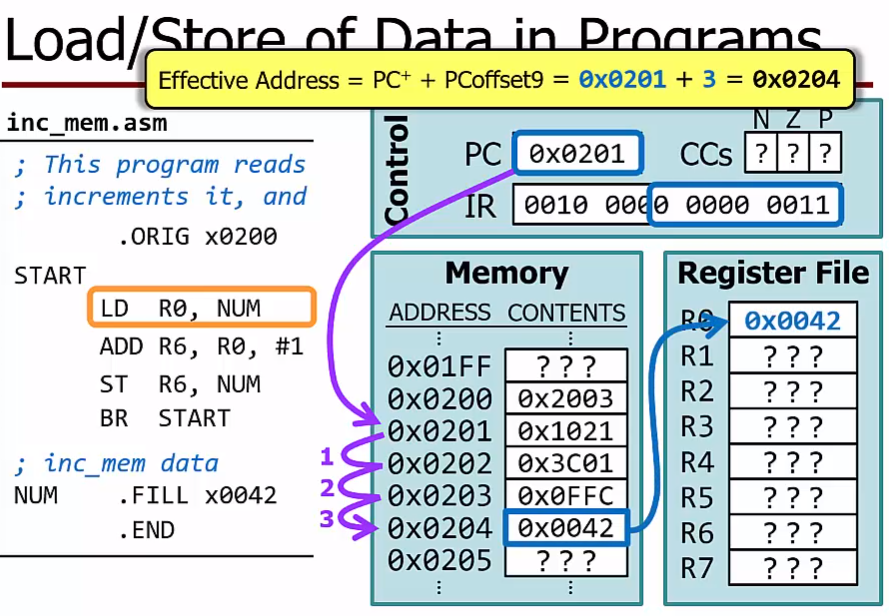
LD function

A load instruction copies a value from a memory location to a register
LD R0，NUM
copy whatever is in the memory location named NUM to register R0

LD DR, label ; Load from mem(PC-relative)

$DR <- mem[PC^+ + SEXT(PCoffset9)], setcc()$

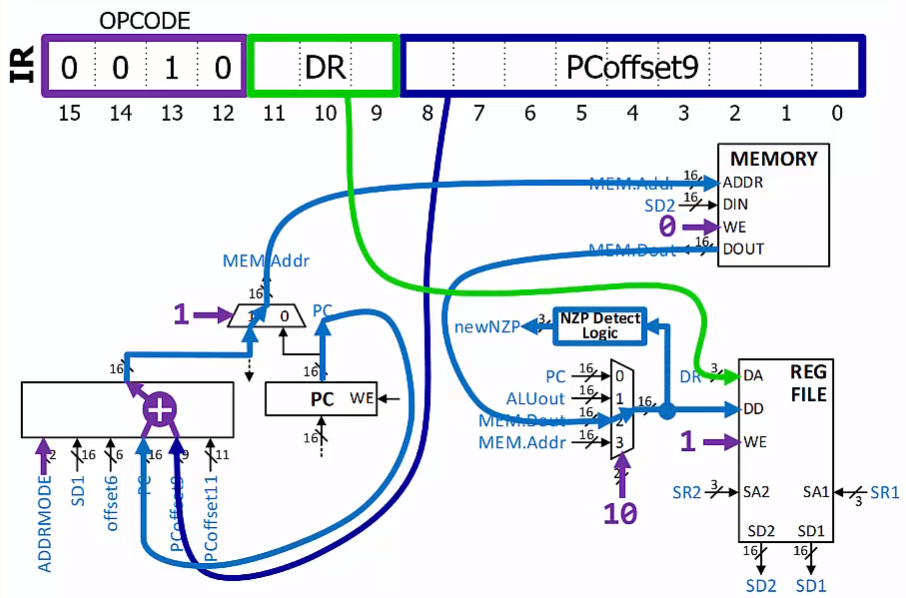
ST function

A store instruction copies a value from a register to a memory location
ST R6，NUM
copy whatever is in register R6 to the memory location named NUM

ST SR, label ; Store to men(PC-relative)

$mem[PC^+ + SEXT(PCoffset9)] <- SR$

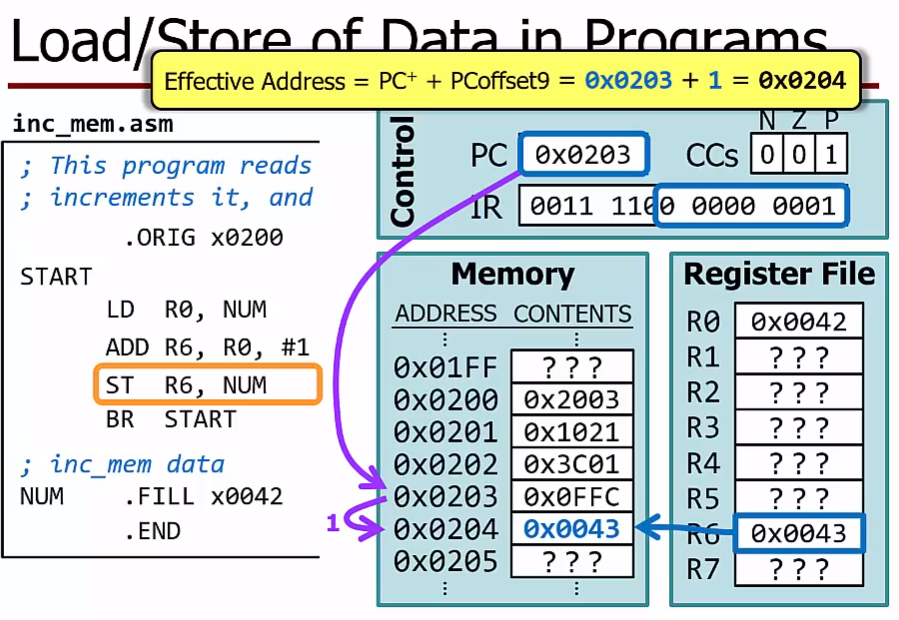
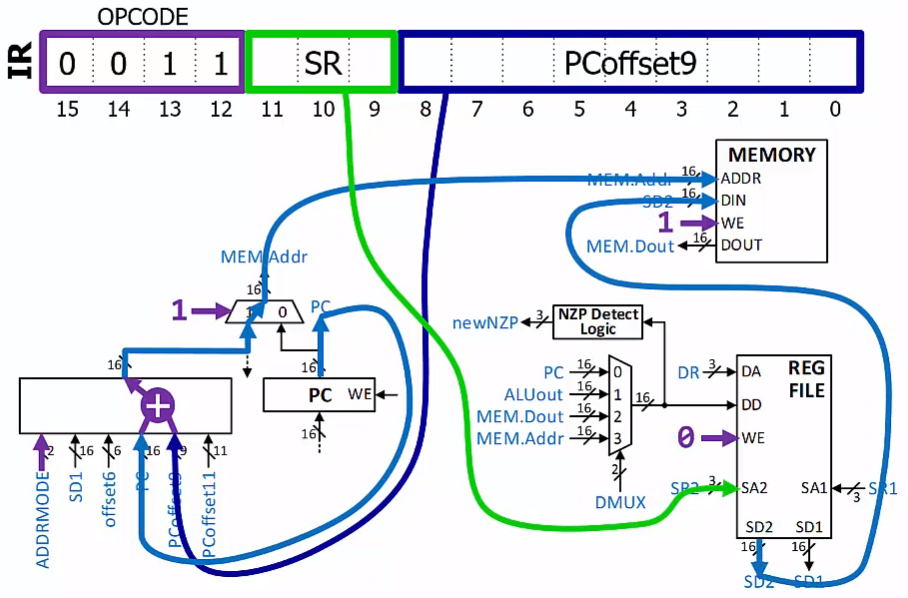
Idea: instead of encoding the actual address, encode how far away it is from where the Program Counter is pointing

• This is called a PC-Relative addressing mode

$PC^+$ used here to mean “already-incremented PC”

These instructions are used for accessing memory “near” the current PC value

• 9-bit 2’s-complement offset means the address must be within [-256,+255] of the already-incremented PC

More Data Movement

LDR and STR use Base+Offset addressing.

The base register acts as a “pointer”into memory.

The signed offset indicates how far away the effective address is from where the base register is pointing

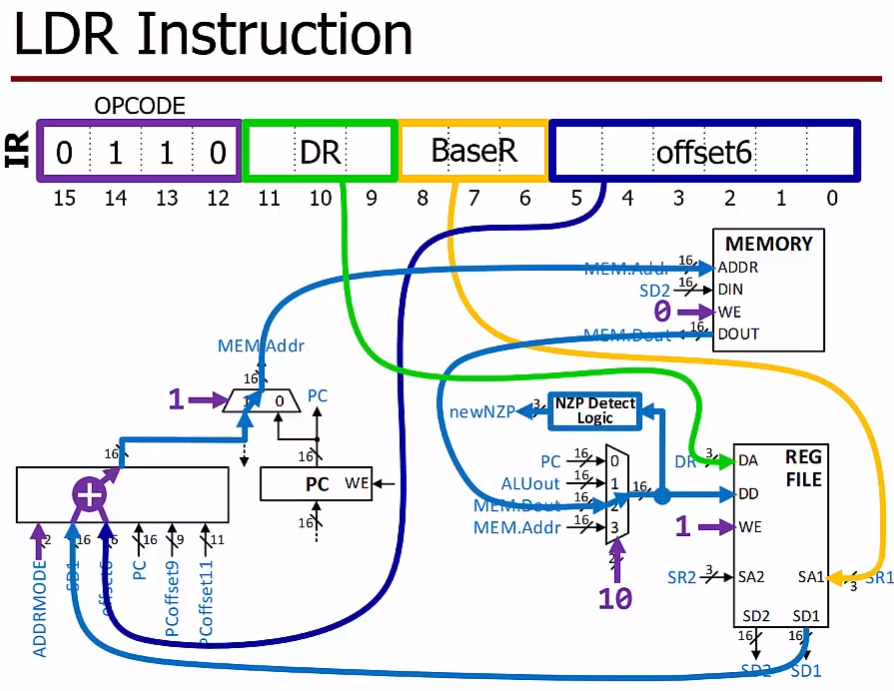
LDR function

LDR R5, R1, #2

read whatever is in memory two steps past the address in R1, and copy it to register R5

LDR DR, BaseR, offset6 ; Load from men (base+offset)

$DR <- mem[BaseR + SEXT(offset6)], setcc()$

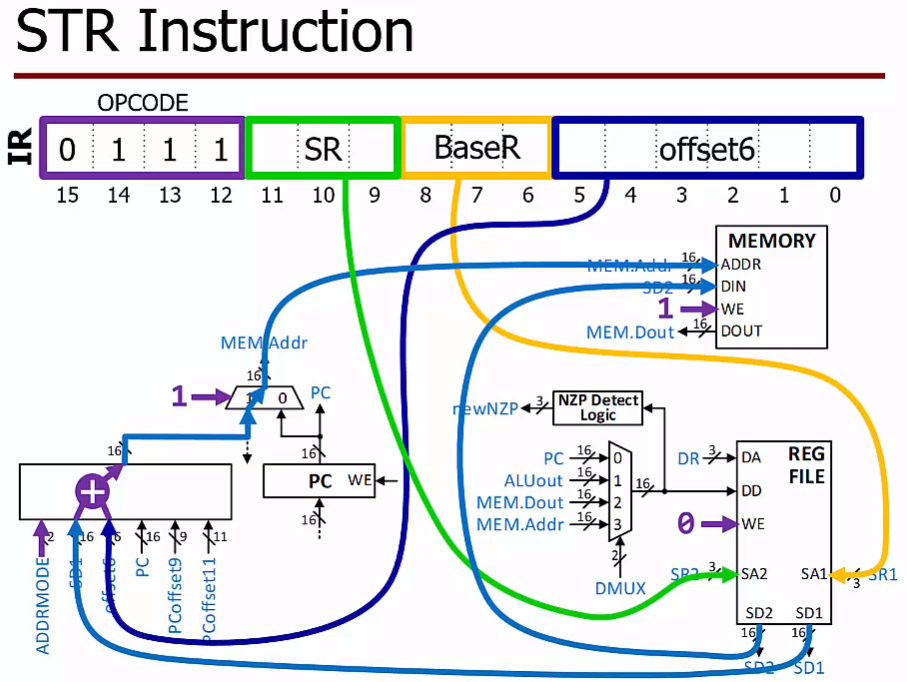
STR function

SRT R5, R1, #2

copy whatever is in register R5 to memory two steps past the address in R1

STR ST, BaseR, offset6 ; Store to men (base+offset)

$men[BaseR + SEXT(offset)] <- SR$

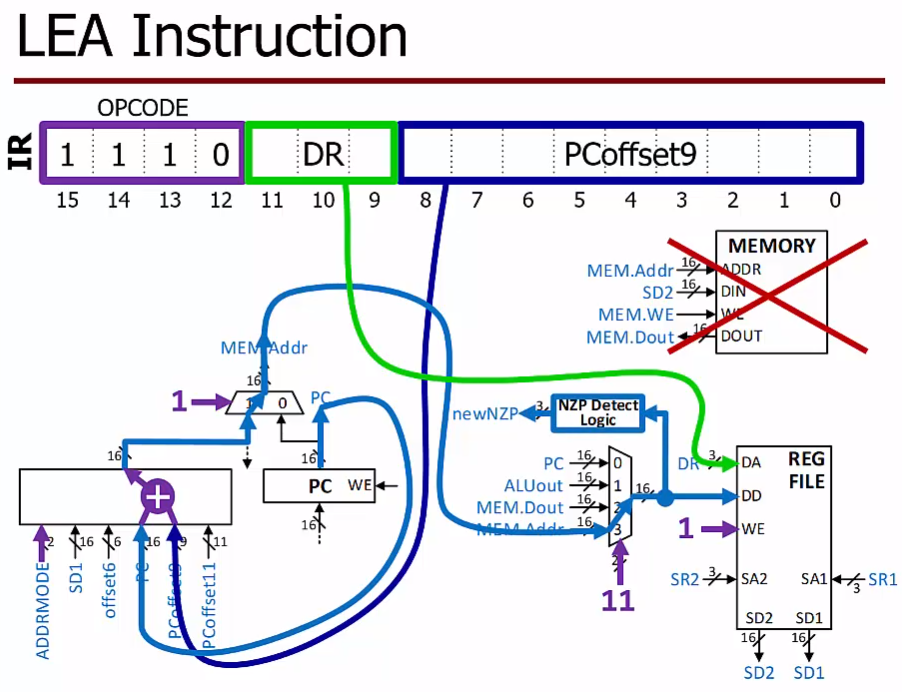
LEA function

LDR and STR are only useful if we first put a useful address into a register!

LEA copies a label’s address to a register

“Load Effective Address”

• The effective address for LEA is calculated exactly the same way as it is for LD and ST (PC-Relative)

LEA DE, label ; Put label address into reg

$DR <- PC^+ + SEXT(PCoffset9), setcc()$

LEA R1, ARRAY

Memory Indirect

LD and ST allow us to access labelled memorylocations “near” the instructions

- The distance is limited by the size of the PC offset field

LDR and STR are more flexible…

Can access locations around a “nearby” label.

- Use LEA to get a label address into the base register
- Then use LDR/STR to access locations at/near base address

Can access any address

  - Use a .FILL directive to create a location holding an address
  - Use LD to load the address from memory

Then use LDR/STR to access locations at/near base address

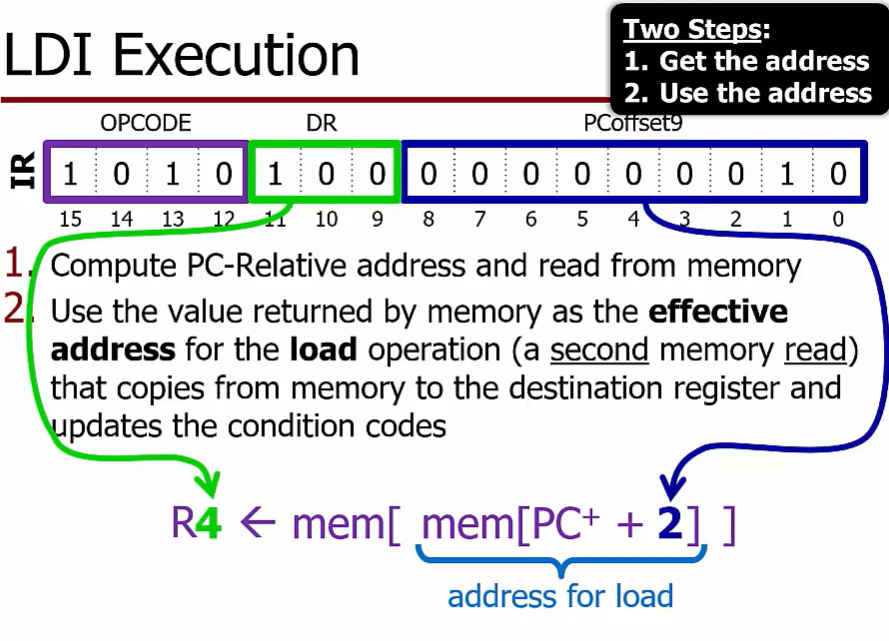
LDI function

read from the location labeled ADDR_R to get the effective address for a load that copies from memory to register R4

Load using Memory Indirect

LD R1, ADDR_R
LDR R4, R1, #0
LDI R4, ADDR_R

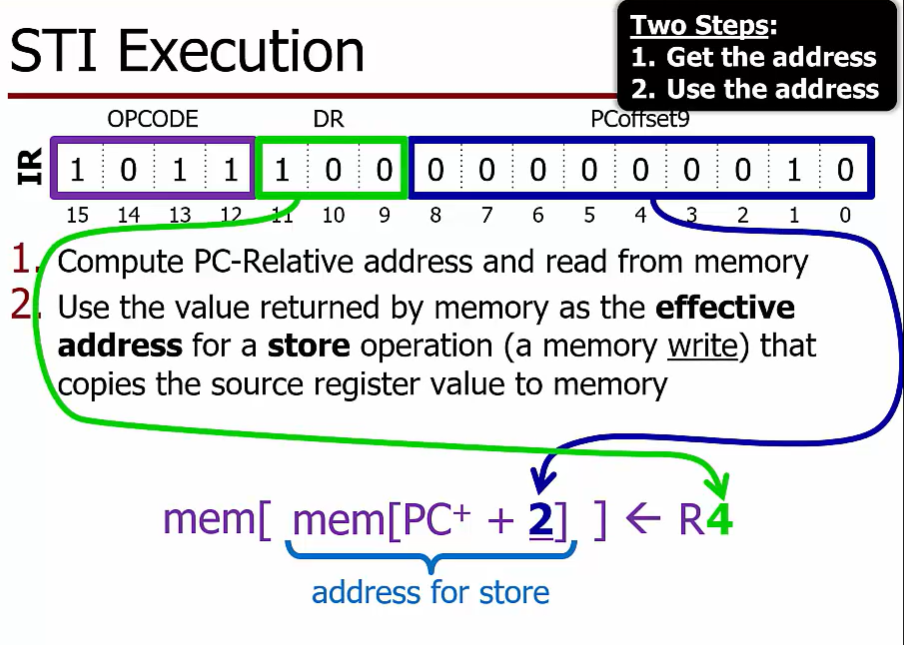
STI function

read from the location labeled ADDR_w to get the effective address for a store that copies from register R4 to memory

Store using Memory Indirect

LD R2, ADDR_W
STR R4, R2, #0
STI R4, ADDR_W

Week09

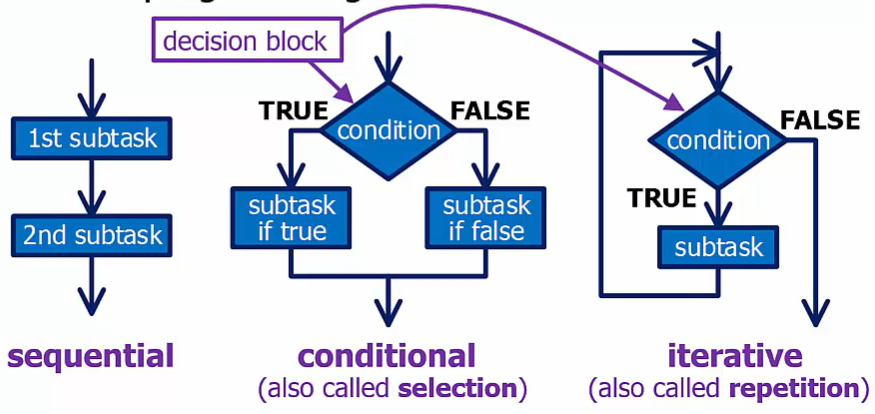
Flow Chart

Flowcharts graphically represent programs during their design

• Writing code for a flowchart is the easy part!

Systematic Decomposition

Break down complex problems into a set of easier-to-handle tasks

Replace each task with set of smaller tasks and condition tests until each step is easy

Changing the Flow

The next instruction to execute does not have to be in the next location in memory

Branch instructions allow the program to change the value in the PC

• Unconditional branch: always updates the PC.
• Conditional branch: only updates the PC(is taken) if some specified condition is true
• If the condition is false, the branch is not taken, and the next
  instruction to execute will be the one at the memory location just after the conditional branch instruction
• The new PC value is called the branch target

BR Instruction

Calculate the branch target by adding the sign-extended offset to the already-incremented PC

Compare conditions indicated in the instruction with the current NZP condition code values.

If any match, then update the PC with the calculated branch target

If none match, do not modify the PC

Note: even if the BR does not modify the PC, the PC was incremented when the BR was fetched

BRx label
; Conditional branch to label, x is condition

$PC <- PC^+ + SEXT(PCoffset9)$

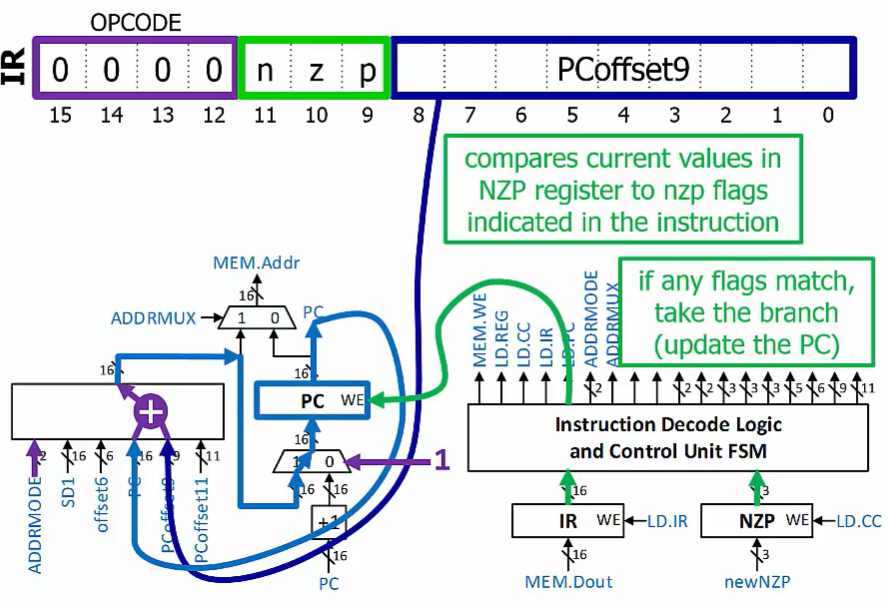
值得注意的是PC是已经incremented的所以指向BR的下一行，offset也是从下一行开始算要加多少行

z =0, zp >= 0, np !=0, nzp= uncnditionally

看的时候只要NZP这三个框有一任意在指令里的是1就行，例如指令是zp，control是NZP 001 符合

JMP

The distance of a BRanch target is limited by the range of offsets encoded in the instruction

• 9-bit offset,range [-256,255] from incremented PC
• If target code is at an address further away in memory,need to use a different instruction…

JMP is an unconditional jump instruction that updates the PC with the value in a register

JMP BaseR ; Jump to address in register

$PC <- BaseR$

Read value from source register

Write the source register value to the PC

Masking

bit从0开始

检查第n位是0，倒着来最低位都是0，第n位是1，$2^{n}$，BRz

检查第n位是1，倒着来最低位都是0，第n位是1，$2^{n}$ ，BRp

检查后几位 011001, 写了n位就是n个1，$2^{n}-1$, ADD R0, R0, #(1-2^n) , BRz

Week10

Assembly Language

Low-level language

• One-to-one correspondence between assembly language instructions and machine instructions

• As in all languages, you have to use correct grammar!

Advantages over machine language

• Mnemonics instead of numeric opcodes: A short sequence of letters that has the same underlying meaning as a specific opcode value, but also hints at what the instruction does.
• Symbolic names instead of numeric addresses
• Encoding of instructions Offsets, immediate values

lables store in symbol table

.ORIG and .END is assembler directives

.BLKW .FILL .STRINGZ is memory allocation directives

Running a Program

Assemble the source code

• Produce a program image (code and initialized data)

Load the program into the memory

• A real processor includes special hardware to write the assembled program binary into memory
• In a simulator, the binary program file is read and copied into the simulator’s model of the memory

Execute the program

• Often want to go through a program one instruction ata time, or run to a certain instruction and pause
• Simulators and hardware debug tools both provide this capability

Debugging

Debuggers usually provide two types of single-step execution that you can use:

• Step into: executes one instruction and then pauses

• Step over: like step into, but if the instruction is a subroutine call, executes the entire subroutine( including any subroutines it calls) before pausing

Breakpoints are another important tool that let you run the program up to a certain instruction.

• You can then check the register and memory values when execution reaches that point, and if needed, single-step from there

Memory Allocation

Allocate: reserve space in memory

• No other variable or code will be placed there

Initialize: set the value in a memory location when program is loaded

• In other words, before the program executes

.FILL value

Allocates one word of memory, initialized to the indicated value when the program is loaded

• The value in that location may be changed later by executing a store instruction
• Optional label can be used to refer to that location

.BLKW count

Allocates count words of memory

BLKW = “BLocK of Words”

The allocated memory locations are not initialized.

They may happen to be 0… or they may not…

.STRINGZ “string”

Allocates and initializes memory to hold a null-terminated character string

• One word per character, where each character is represented by its ASCII code
• Last location holds the value 0 to indicate end of string.
  • This is the ‘z’ in STRINGZ
  • Also called the “null terminator”

Total allocated words = number of characters plus 1

Week11

Subroutines

Subroutines are well-defined software modules that are written to perform a specific task

• Functions and methods in high-level languages are implemented using subroutines

To use a subroutine, a program calls the subroutine

• The processor executes the subroutine code
• When the subroutine code is finished, the processor returns to the next instruction after the one that called the subroutine

A program can call a subroutine multiple times. Subroutines can also call other subroutines

More abstract approach to programming by encapsulating lower-level tasks

• Code calling the subroutine does not need to know the details of how the subroutine code actually works

Write modular code to simplify testing and increase possibilities for software reuse

• Testing a small subroutine is much simpler than testing an entire program

JSR

R7 <- already-incremented PC

PC <- address of label

If a subroutine calls another subroutine (or otherwise modifies R7), it MUST save a copy of R7 to memory before calling the subroutine, and then restore R7 before its RET instruction

Parameter Passing

Many subroutines require information from the caller to perform their task, and may need to return one or more results to the caller

• Commonly called parameters

Parameters can be passed to and from the subroutine in a variety of ways

• In registers
• In specific memory locations.
• On the stack
• A special data structure implemented in most processors

Pass-By-Value: value store in the register

Pass-By-Reference: address store in the register

Caller-save & Callee-save

Caller-save: the caller code is responsible for saving/restoring any needed register values.

• Store the values in those registers to memory before calling the subroutine
• Re-load the saved values after the subroutine returns

在调用子函数之前存好register

Callee-save: the subroutine is responsible for saving/restoring any modified register values.

• Subroutine must appear to not modify registers.
• …..except for those used to hold results
• ….and the register that holds the return address (R7)!

Referred to as context save and restore

Disadvantage:
. The subroutine may unnecessarily save/restore registers that the caller is not using

Advantages:
. Only a single copy of the register save/restore code is present,regardless of how many times the subroutine is called
· Callers can freely use subroutines, knowing that the subroutine will not corrupt any registers

Callee-save is normally used (with one exception). A caller must save R7 before calling a subroutine,since that call will overwrite the value in R7

Week13

I/O concept

General-purpose I/O (GPIO) pins

• The most basic form of output is a pin that the processor can set to 1 or 0 (voltage levels). Turn a light ON or OFF

• The most basic form of input is a pin that the processor can be read to determine its voltage level (1 or 0)

• Check if a button is pressed or not

Analog-to-digital converter ( input device)

• Sample an analog signal and represent it as binary data

Digital-to-analog converter (output device)

• Convert digital (binary) data into an analog signal

Complex I/O Devices

Most devices operate as both input and output

• Network interface
• Bluetooth radio
• USB interface
• Hard drive

I/O Synchronization

Processors run at a rate controlled by the clock

But, most I/O activity occurs at unpredictable times unrelated to the processor clock

• Example: Someone typing on a keyboard

This is asynchronous I/O

• Asynchronous means “not related to the clock”

For the processor to operate with asynchronous I/O devices, there must be a way for the processor to check if the device needs service

Unconditional / Conditional

Some simple I/O devices are always ready to accept or supply new data

For most I/O devices, we need to check if they are ready before transferring data

Isolated / Memory - Mapped I/O

Some processors use special instructions and a different address space to do this

• This is isolated I/O

Most processor use their normal load/store instructions to access I/O devices

• To the processor, the I/O device registers appear to be normal memory locations… but they are not!

• We set aside some locations in the memory space, and add logic so that loads/stores to these addresses access the I/O device registers instead of memory

Polled / Interrupt-Driven I/O

Polling is the process of repeatedly checking to see when something becomes ready

For example: we poll the keyboard to see if it has anew character; the answer is “no” until one is typed!

Processors also contain hardware that allows an I/O device to interrupt the processor

When I/O operations use interrupts, the I/O device announces to the processor (without the processor asking) that something has happened.

On the other hand, when I/O operations use polling, the processor repeatedly asks the I/O device if something has happened.

I/O Device Interface

Status registers: processor reads to check device state

• A keyboard sets a status register bit to indicate data is ready

Data registers: used for the exchange of data

• when a key is typed, a keyboard places the corresponding ASCII code in a data register for the processor to read

Control registers: processor writes to change how the I/O device operates

• A keyboard may have a backlight that the processor can turn off to save power when the computer is idle
• The processor may change the operating speed of a serial communications port

The data provided by a memory-mapped input device can be accessed by reading from the device’s memory-mapped Data Register

Data can be sent to a memory-mapped output device by writing to the device’s memory-mapped Data Register

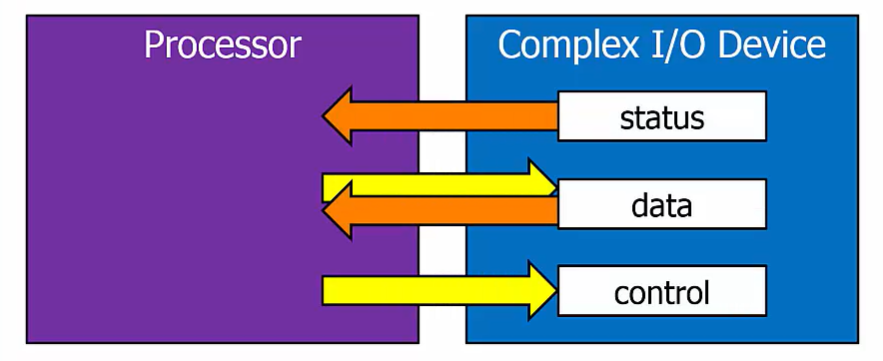
LC-3 I/O

Keyboard Input

Registers:

Keyboard Status Register (KBSR) address = 0xFE00

• KBSR[15] is 1 if a new character is available, 0 otherwise.
• This use of KBSR[15] is a synchronization mechanism, and we refer to KBSR[15] as a flag that indicates if information is available.

Keyboard Data Register (KBDR) address = 0xFE02

• KBDR[7:0] contains the ASCII code of the last character typed
• Reading KBDR automatically resets bit 15 of the KBSR

Usage:

• To check if a character is available, read KBSR and test if bit 15 is 1. Is the value negative?

When a character is available, read it from KBDR

Read from KBSR, Get the value from KBDR, (address KBDR = KBSR + 2)

LD    R1, IO_BASE    ; start of memory-mapped I/O
WAIT            ; start of Poiling Loop
    LDR    R2, R1, #0
    BRzp    WAIT
    LDR    R0, R1, #2

Character Display Output

Registers:

Display Status Register (DSR) address = 0xFE04

• DSR[15] is 1 if the display is ready, 0 otherwise

Display Data Register (DDR) address = 0xFE06

• The character (ASCII code) written to the DDR will be displayed on the screen

Usage:
To check if the display is ready to accept a character,read DSR and check if bit 15 is 1

When the display is ready, write the character to DDR

LD    R1, IO_BASE ; start of memory-mapped I/O
WAIT
    LDR    R2, R1, #4    ; read from DSR +4
    BRzp    WAIT
    STR    R0, R1, #6    ; write to DDR +6

LDI/STI

The book uses LDI and STI for its examples; this video instead uses LD+LDR and LD+STR

• LDI is equivalent to LD followed by LDR
• STI is equivalent to LD followed by STR

Using LDI in a polling loop means two memory reads foreach iteration instead of one

• Remember - memory accesses are actually very slow…
• Why read memory repeatedly to get the status register address?
  • We only read the IO_BASE address once, then use LDR/STR instructions with the appropriate offsets

Most modern processors do not have LDI/STI

• Performance issues outweigh any benefits
• Included because the idea of indirect access is important

OS

Allows applications to interact with I/o devices without having to have specific knowledge of all possible I/O devices

• Keyboard/mouse/pen/touchscreen input.
• Display/printer output
• Disk access
• Network access

All application-level I/0 is controlled by and goes through the os

• The system hardware usually prevents applications from accessing the I/O directly to ensure this

communicating with the OS: Need a mechanism that insulates the OS from the application (and vice-versa), but allows the
application and the OS to communicate

• Must be built into the processor itself so it cant be circumvented by malicious software

Processors provide an indirect mechanism for apps to request OS services

These are special instructions called software interrupts or traps

• Part of the instruction is a code used to identify the specific type of service requested
• Executing these instructions is a “system call”

These instructions transfer control to the operating system, which performs the service and then returns control to the application

LC-3 Operating System

How does the LC-3 processor access I/O devices?

• By interacting with memory-mapped I/O device registers.

A memory-mapped device register is a special register that is physically located somewhere outside of the memory and register file.

To use LC-3 OS services, you must assemble and load the LC-3 OS before loading your program

• Processor still starts execution at 0x0200, but now that location is part of the OS code
  The OS jumps to 0x3000 to run your program, so your program needs to start there when using the OS

The TRAP instruction requests an OS service.

• OS executes a service routine or TRAP handler

• Returns to your program when finished

The LC-3 OS provides some basic I/O services.

• Reading from the keyboard
• Writing to the console display

TRAP

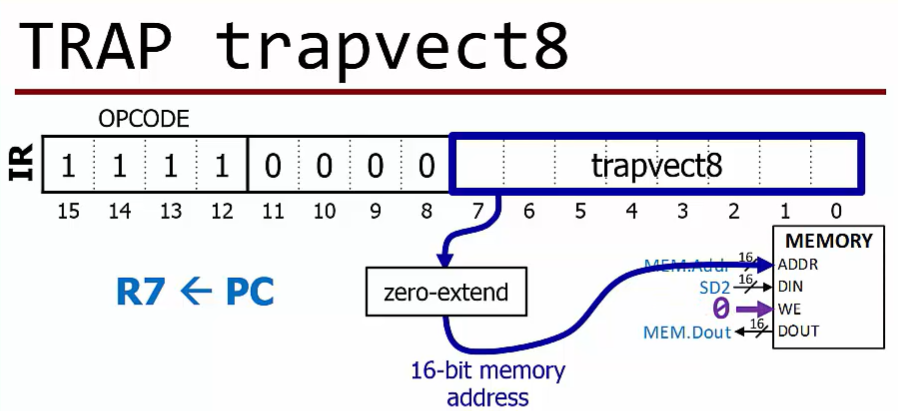
• Copy PC to R7

• Zero-extend 8-bit code to use as address for reading from the vector table.

• Addresses 0x0000-0x00FF

• Value returned from table is written into PC
  . The address of requested TRAP handling routine

• TRAP handlers return just like subroutines do
  · All handlers end with RET

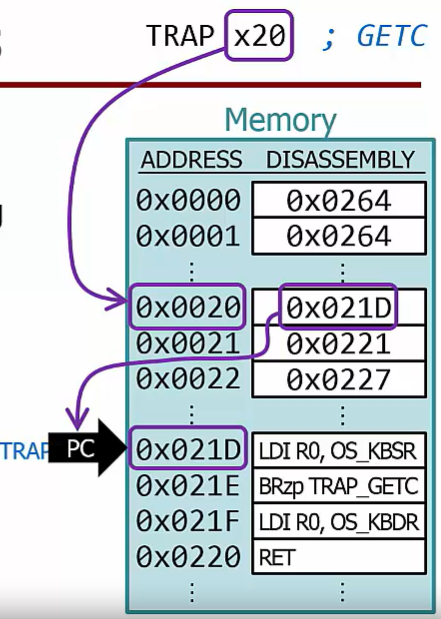
Uing TRAPS

Since TRAP uses R7 to hold the return address, code using R7 must save and restore it
There are six service routines, and the LC-3 assembler supports an alias for each

• GETC TRAP x20 Waits for a character from the keyboard. ASCII code returned in R0[7:0]

• OUT TRAP x21 Writes a character to the console display. ASCII code passed in R0[7:0]

• PUTS TRAP x22 Writes an ASCIIz string to the console display. String address passed in R0

• IN TRAP x23

• Writes “Input a character>” to console display,then waits for a character from the keyboard.

  ASCII code returned in RO[7:0]
  Character is also echoed to the console display

• PUTSP TRAP x24 not used in ECE 252

• HALT TRAP x25 transfer control to OS and restart