大二复习
基础数学
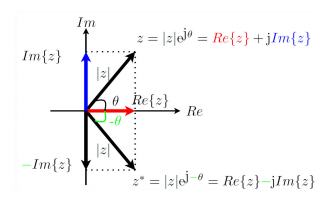
$e^{j\theta}=cos(\theta)+jsin(\theta)$
$cos(\theta)=\frac{e^{j\theta}+e^{-j\theta }}{2}$
$sin(\theta)=\frac{e^{j\theta}-e^{-j\theta }}{2j}$
$$
\sum_{n=0}^{\infty}{(z_0)^n=\frac{1}{1-z_0}} ,|z_0|<1
$$
连续信号与离散信号
信号的分类
$$
E_{\infty}=\int_{-\infty}^{\infty}|x(t)|^2dt
=\sum_{n=-\infty}^{\infty}|x[n]|^2
$$
$$
P_{\infty}=\lim_{N \rightarrow \infty}\frac{1}{2T}\int_{-T}^{T}|x(t)|^2dt=
\lim_{N \rightarrow \infty}\frac{1}{2N+1}\sum_{-N}^{N}|x(t)|^2
$$
- 有限能量信号(Finite‐energy signal):$E_{\infty}<\infty,P_{\infty}=0$
- 有限功率信号(Finite‐power signal):$P_{\infty}<\infty,E_{\infty}=\infty$
- 无限功率能量信号(Infinite energy & power signal ):$P_{\infty}\rightarrow\infty,E_{\infty}\rightarrow\infty$
信号的偶部与奇部
$x(t)=x_e(t)+x_o(t)$
$x_e(t)=E_v[x(t)]=1/2[x(t)+x(-t)]$
$x_o(t)=O_d[x(t)]=1/2[x(t)-x(-t)]$
信号的频率与周期
对于连续信号$x(t)=e^{jw_0t}$,有$\frac{2\pi}{|k|w_0}=\frac{T_0}{|k|}$
对于离散信号$x[n]=e^{jw_0n}$有$\frac{w_0}{2\pi}=\frac{m}{N}$,周期满足$N=m(2\pi/w_0)$ 整数
区别就是离散信号N一定为正整数
基础信号
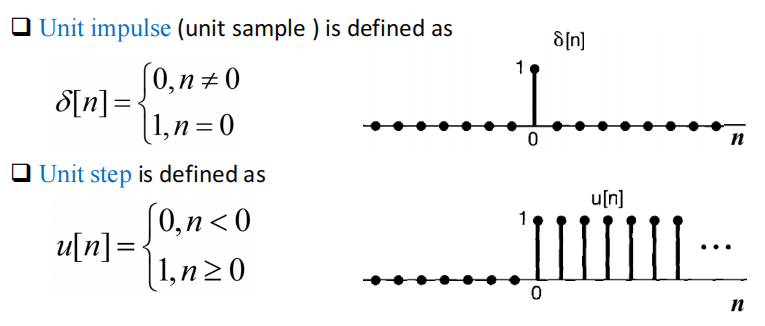
单位脉冲信号与单位阶跃信号
离散时间的定义
一些性质
- $\delta[n]=u[n]-u[n-1]$
$u[n]=\sum_{m=\infty}^{n}\delta[m]$
$x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]$
连续时间的定义:
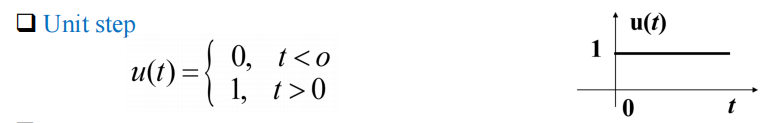
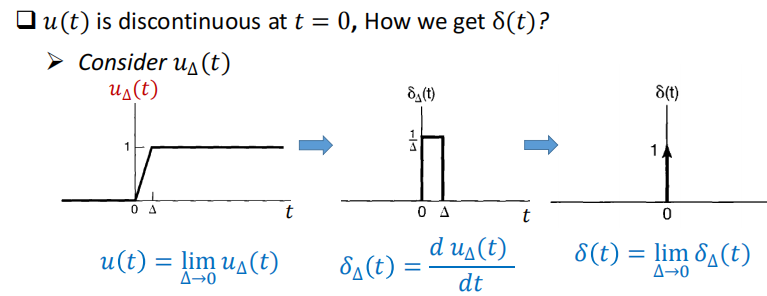
一些性质:
- $u(t)=\int_{-\infty}^{t}\delta(\tau )d\tau$
- $\delta(t)=\frac{du(t)}{dt}$
- $x(t)\delta(t-t_0)=x(t_0)\delta(t-t_0)$
基本信号的性质
记忆系统:输出决定于现在和以前的输入,(不管将来)非记忆就是只和现在状态相关
例子:$y[n]=\sum_{k=-\infty}^{n}x[k],y[n]=x[n-1]$
可逆性:不同输入对应不同输出
例子:$y[n]=0,y(t)=x^2(t)$不可逆
因果性:任何时间的输出都只由现在和以前的状态决定,注意和记忆区别
例子:$y[n]=x[n]-x[n+1],y(t)=x(t+1)$非因果
稳定性:输入有界,则输出有界一定稳定
时不变性:时间平移造成相同的输出平移
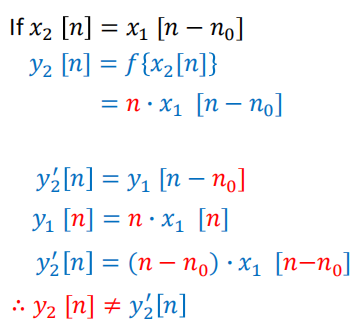
线性:$x_1(t)->y_1(t),x_2(t)->y_2(t)$有$ax_1(t)+bx_2(t)->ay_1(t)+by_2(t)$
易错例子:
$y(t)=\frac{dx(t)}{dt}=\lim_{\Delta t \rightarrow 0}\frac{x(t+\Delta t)-x(t)}{\Delta t}$
是记忆,不可逆,非因果,不稳定,时不变,非线性系统(因果用定义判断)
卷积(Convolution)
定义
已知x,y系统的关系,求$h(t)$就是把$x$换成$\delta$
离散时间
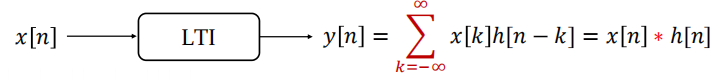
例子:
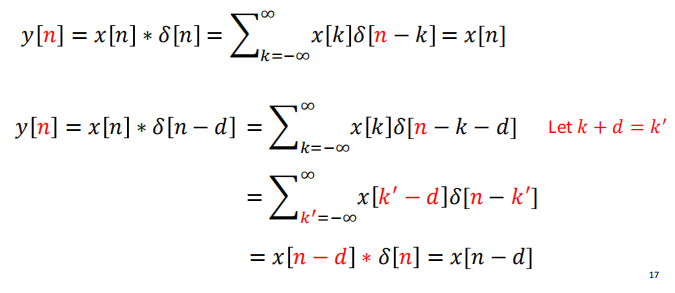
连续时间
$\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau=x(t)*h(t)$
同理
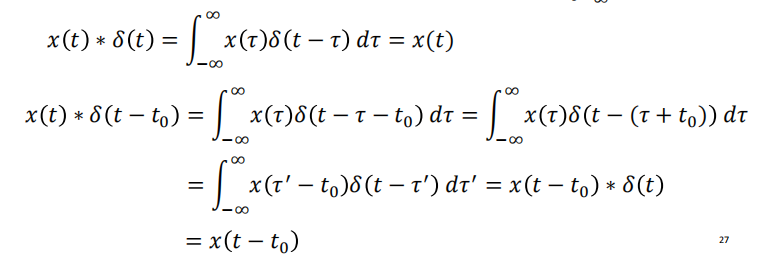
计算
核心:以$t/n$的大小分类讨论
一般习惯用画图法,画出$h(t-\tau)$的图来和$x(\tau)$相乘分类讨论
例子如下:

若$h(t)=f(-t+a)$则画图时候还是处理成$\tau$不用取反,位移看成$h(\tau-(t-a))$,于是对应的位移坐标是$t-a$
性质
以连续时间为例子,离散时间同理
交换律: $x(t)h(t)=h(t)x(t)$
分配律: $x(t)(h_1(t)+h_2(t))=x(t)h_1(t)+x(t)*h_2(t)$
结合律: $x(t)(h_1(t)h_2(t))=(x(t)h_1(t))h_2(t))$
当且仅当$h(t)=0,\forall t \neq 0$,该系统是没有记忆的很好理解因为$x(t)*h(t-\tau)$ 要保证$h(t-\tau)$只有$h(t)$有值
如果$h_0(t)*h_1(t)=\delta(t)$则$h_1(t)$是$h_0(t)$的逆系统
例子:$y(t)=x(t-t_0)$逆系统表达$y_1(t)=x(t+t_0)$因为 $\delta(t-t_0)\delta(t+t_0)=\delta(t)$对应$h(t)h_1(t)=\delta(t)$
当$h(t)=0 ,t<0$时,$y(t)=x(t)*h(t)$系统是因果的
这个条件相当于$h(t-\tau)=0,t-\tau <0$
当$h(t)$绝对可积,则该系统稳定$\int_{-\infty}^{\infty}|h(\tau)|d\tau < \infty$
单位阶跃响应$s(t)$就是把$x(t)=u(t)$计算得到的值,即$s(t)=\int_{-\infty}^th(\tau)d\tau$
差分与求导
本质好像就是求微分方程,先根据形式猜测特解,再找出齐次通解,最后用条件求解


注意课件上最后带入的时候写错了,负号消失了
至于差分就是等比\等差数列求解
然后有一个画图表示的
傅里叶系数(Fourier Series Representation )
前置信息
当输入是负数信号时候输出的形式,引入LTI系统中$H(s)$的概念

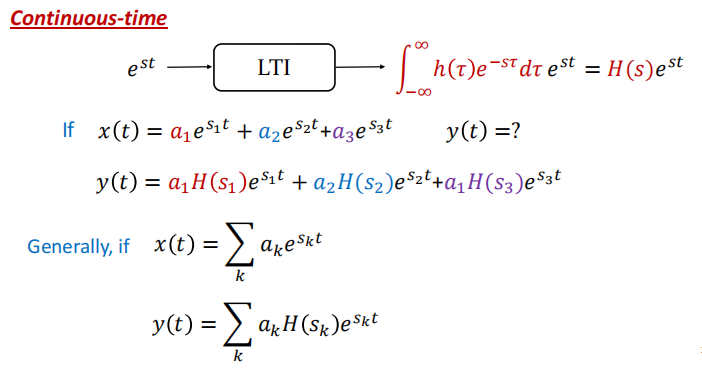
离散时间同理
定义
前面提到输入是复数信号的输出形式有一种比较便捷的表达形式,那么如何将任意$x(t)$改写成复数信号的线性组合呢,我们引入傅里叶级数
连续时间:
$$
x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jk(2\pi /T_0)t}
$$
这里的$a_k$就是傅里叶级数,$w_0=2\pi/T_0$
若$x(t)$是实信号,有另一个表达方法
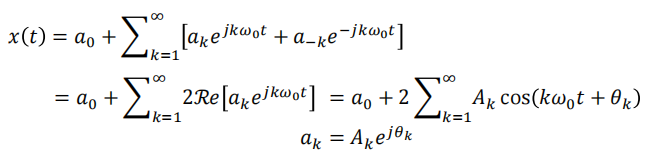
利用的是$a_k=a_{-k}^*$的性质
离散时间:
$$
x[n]=\sum_{k=
$$
计算方法
已知$x(t)$如何求$a_k$,有公式
$$
a_k=\frac{1}{T}\int_Tx(t)e^{-jkw_0t}dt
$$
其中
$$
a_0=\frac{1}{T}\int_Tx(t)dt
$$
离散时间:
$$
a_k=\frac{1}{N}\sum_{k=
$$
ps:写答案的时候,$a_k=0$的情况也要写出来,不能不写
例子:常见信号的傅里叶级数,方波,记下来比较好
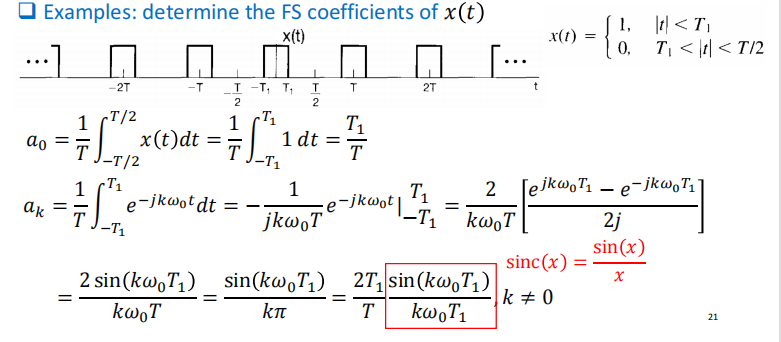
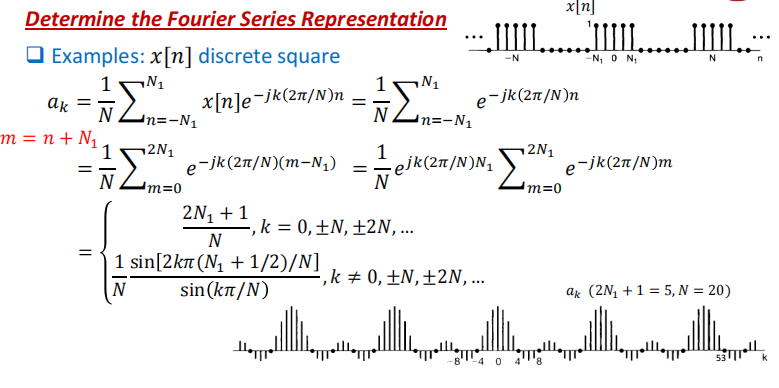
离散时间的方波:
收敛性
不是所有信号都有傅里叶级数,若级数趋于无穷则无法准确表示该信号,故要判断$x(t)$的收敛性
- 条件1:有限能量条件$\int_T|x(t)|^2dt<\infty$,则可以用傅里叶级数
- 条件2:迪利克雷条件:1.绝对可积$\int_T|x(t)|dt<\infty$2.在任意有限时间,$x(t)$有界,满足有限个的最大最小值点。3.任意有限时间,只有有限的点是不连续的。
性质
仍然以连续时间为例子,以下表示傅里叶级数,性质将简化处理
线性:$Ax(t)+By(t)\to c_k=Aa_k+Bb_k$
时间平移:$x(t-t_0)\to b_k=e^{-jkw_0t_0}a_k$
时间反转:$x(-t)\to b_k=a_{-k}$
时间翻倍:$x(\alpha t)\to b_k=a_k,w=\alpha w_0$只改变频率
相乘:$z(t)=x(t)y(t)\to h_k=\sum_{l=-\infty}^{\infty} a_lb_{k-l}$
共轭:$z(t)=x^(t)\to b_k=a^_{-k}$
$x(t)$实信号,$a_k^*=a_{-k}\to |a_k|=|a_{-k}|$
$x(t)$实且偶信号,$a_k=a_{-k}\to a_k=a_k^*\to a_k$实且偶
$x(t)$实且奇信号,$a_k=-a_{-k}\to a_k=-a_k^*\to a_k$纯虚且奇
求导与积分:$dx(t)/dt \to jkw_0a_k;\int_{-\infty}^{t}x(\tau)d\tau \to a_k/(jkw_0)$
频率移动:$e^{jMw_0t}x(t) \to a_{k-M}$
卷积:$\int_Tx(\tau)y(t-\tau)d\tau \to Ta_kb_k$
帕斯瓦尔关系式:$\frac{1}{T}\int_T|x(t)|^2dt=\sum_{k=-\infty}^{\infty}|a_k|^2$
傅里叶级数与LTI系统
与part1结合,我们可以利用傅里叶级数算出输出信号的傅里叶级数表达形式
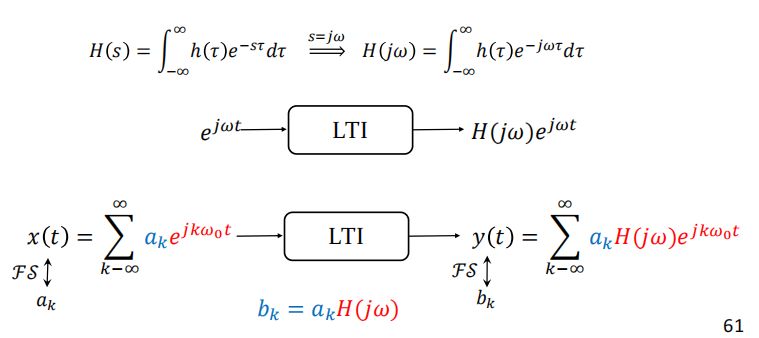
注意其中$w=kw_0$ 带数据不能带错了
傅里叶变换( Fourier Transform)
傅里叶级数表示的都是周期信号,那每周期信号如何处理,我们引入傅里叶变换。
傅里叶变换的思路是将没有周期的信号扩展成周期信号,再对这个周期信号求傅里叶级数,因为原信号没有周期可以引入$X(jw)=\int_{-\infty}^{\infty}x(t)e^{-jwt}dt$
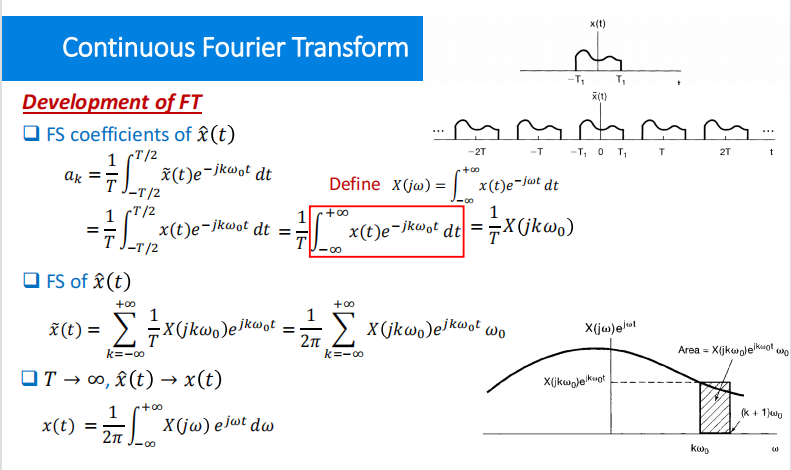
故得到
$$
X(jw)=\int_{-\infty}^{\infty}x(t)e^{-jwt}dt
$$
$$
x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(jw)e^{jwt}dw
$$
$X(jw)$称作频谱(spectrum)
对比FT和FS有$a_k=\frac{1}{T}X(jw),w=kw_0 $
关于收敛性和上述一致,不再重复讨论
一些典型例子
指数型:
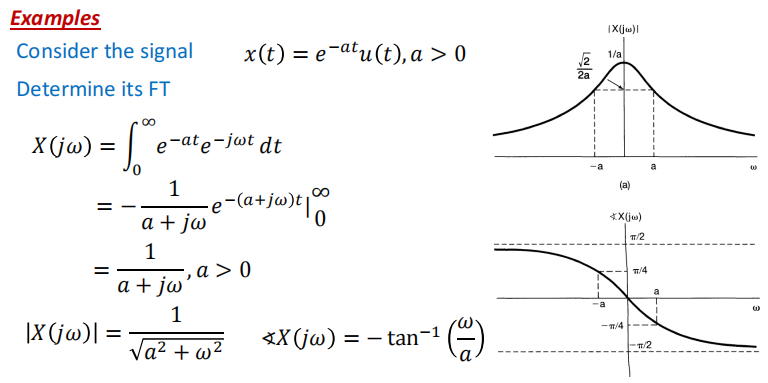
绝对值指数型:
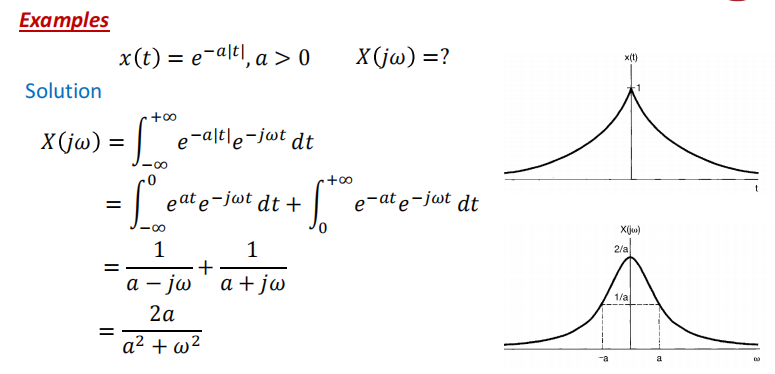
方波型:
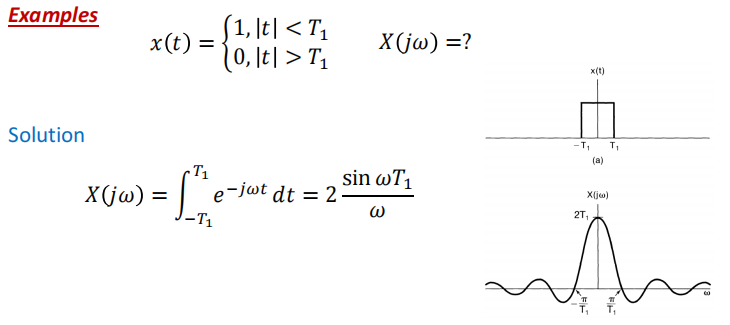
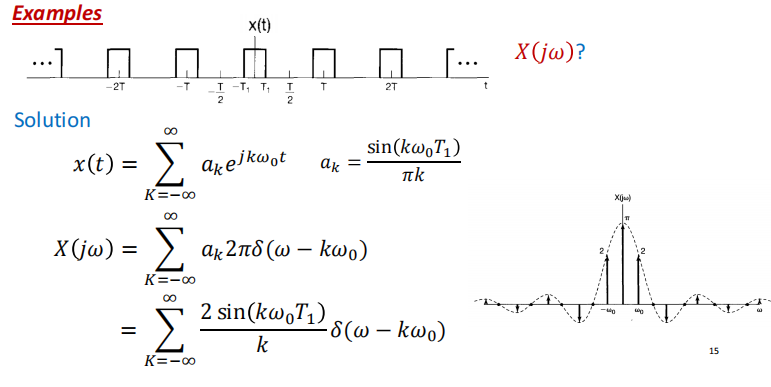
周期信号的傅里叶变换
寻找$a_k$和$X(jw)$的关系

反正得到结论是
$$
X(jw)=\sum_{K=-\infty}^{\infty}a_k2\pi\delta(w-kw_0)
$$
还是方波的例子:
正弦和余弦信号:
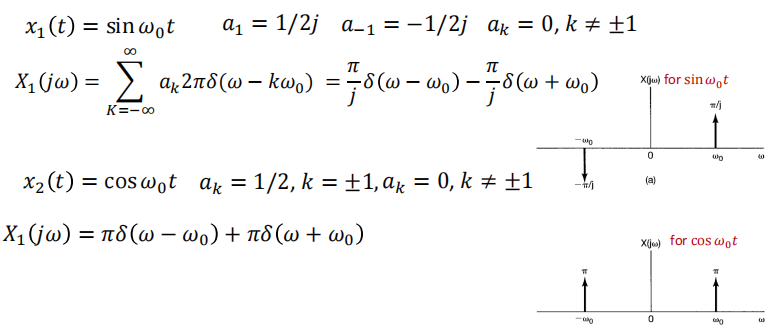
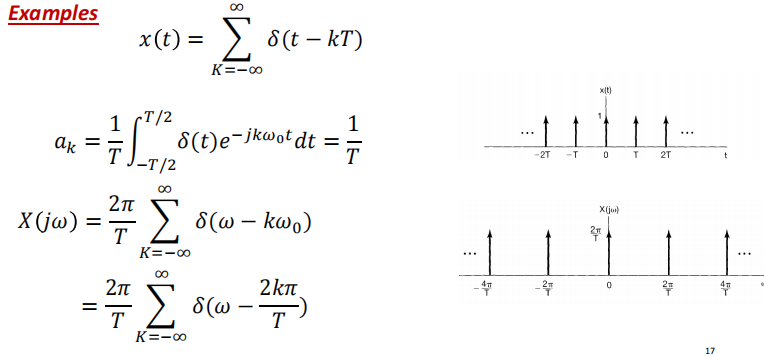
性质
和傅里叶级数有很多类似性质,以下为简化记录
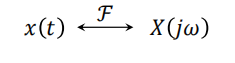
线性:$ax(t)+by(t)\to aX(jw)+bY(jw)$
时间平移:$x(t-t_0)\to e^{-jkwt_0}X(jw)$
时间反转:$x(-t)\to X(-jw)$
共轭:$z(t)=x^(t)\to X^(-jw)$
$x(t)$偶信号,$X(jw)=X(-jw)$,$x(t)$实信号,$X(-jw)=X^*(jw)$
$x(t)$实且偶信号,$X(j w)$实且偶
$x(t)$实且奇信号,$X(j w)$纯虚且奇
$x(t)$实信号,$E_v[x(t)] \to R_e[X(jw)],O_d[x(t)]\to j I_m[X(jw)]$
求导与积分:$dx(t)/dt \to jwX(jw);\int_{-\infty}^{t}x(\tau)d\tau \to \frac{1}{jw}X(jw)+\pi X(0)\delta(w)$
翻倍:$x(at)\to\frac{1}{|a|}X(jw/a),a \neq 0$
帕斯瓦尔关系式:$\int_{-\infty}^{\infty}|x(t)|^2dt=\frac{1}{2\pi}\int_{-\infty}^{\infty}|X(jw)|^2dw$
对偶性:
已知$x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(jw)e^{jwt}dw$
$x(jw)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(t)e^{jwt}dt$
$x(-jw)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(t)e^{-jwt}dt$
例子:

卷积性质
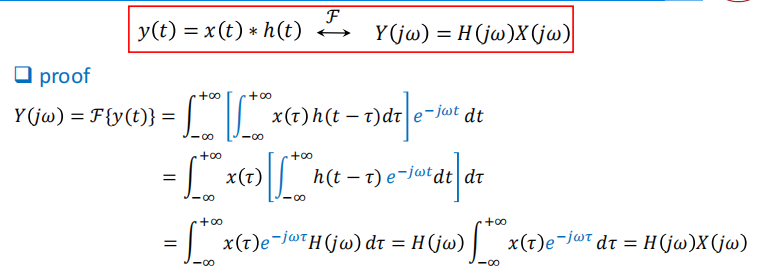
一个比较特殊的$h(t)=\int_{-\infty}^t\delta(\tau)d\tau=u(t)$
$H(jw)=1/jw+\pi \delta(w)$
乘积性质

微分方程
一阶导数,两边都做傅里叶变换来求
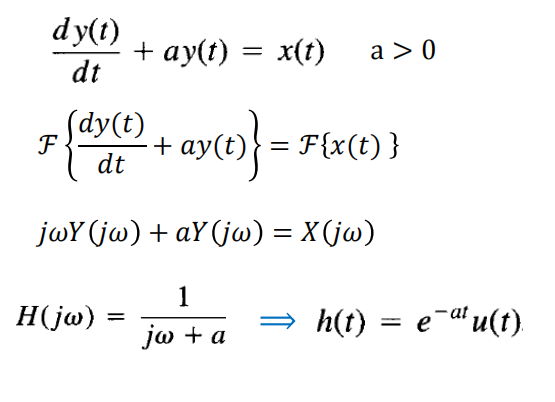
二阶的
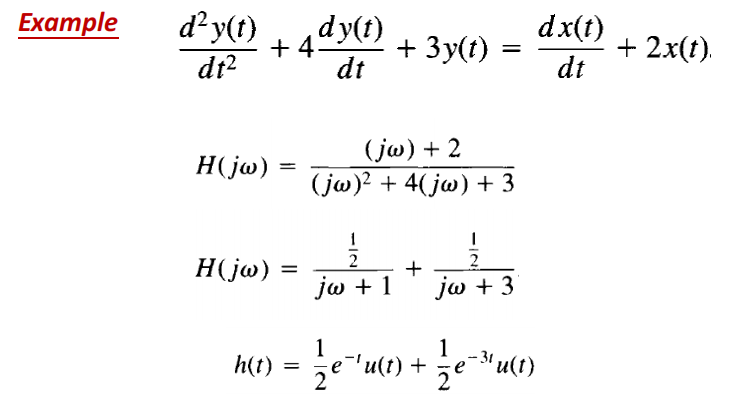
相位与相角
$\angle H(jw)$计算方法,基本分数形式就是分母的相角减去分子的相,若有乘法就是加
$H(jw)=|H(jw)|e^{j\angle H(jw)}$
例子:$ H(jw)=\frac{jw+2}{(jw)^2+4(jw)+3},$ $tan \theta=\frac{w}{2}-\frac{4w}{3-w^2}$
$arg(H(jw))=arctan[\frac{w}{2}-\frac{4w}{3-w^2}]$
group delay:$\tau (w)=-\frac{d}{dw}[\angle H(jw)]$
Log-Magnitude and Bode Plots
在卷积中相角的应用
$y(t)=x(t)*h(t)$ $Y(jw)=H(jw)X(jw)=|H(jw)||X(jw)|e^{j(\angle H(jw) + \angle X(jw))}$
$\angle Y(jw)= \angle H(jw)+ \angle X(jw)$两边取log
$log|Y(jw)|=log|H(jw)|+log|X(jw)|$
波得图(Bode plot):一阶系统
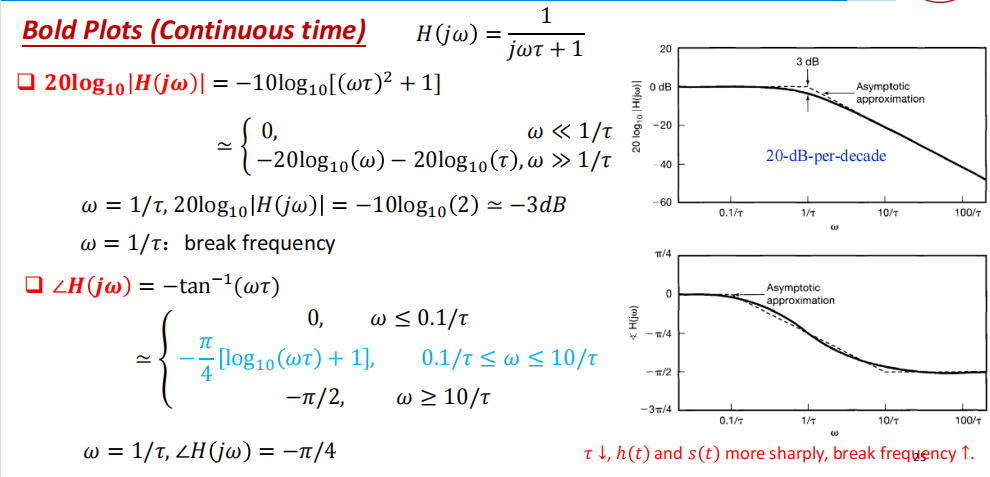
二阶系统
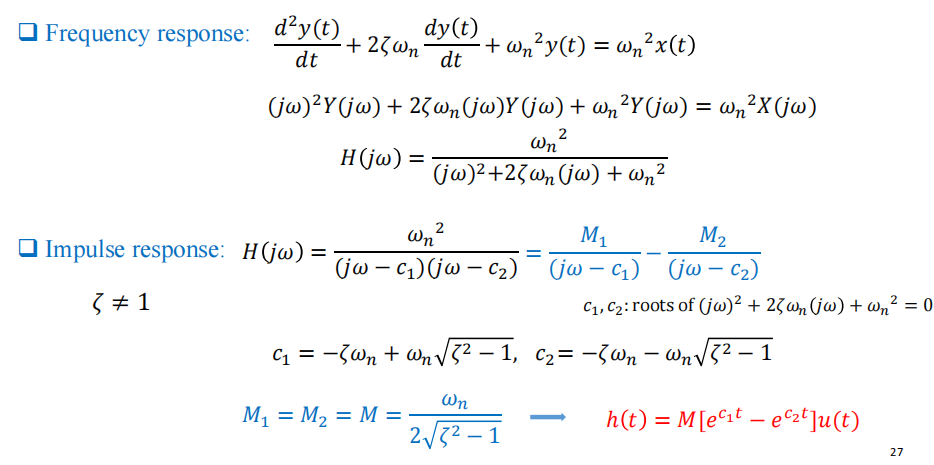
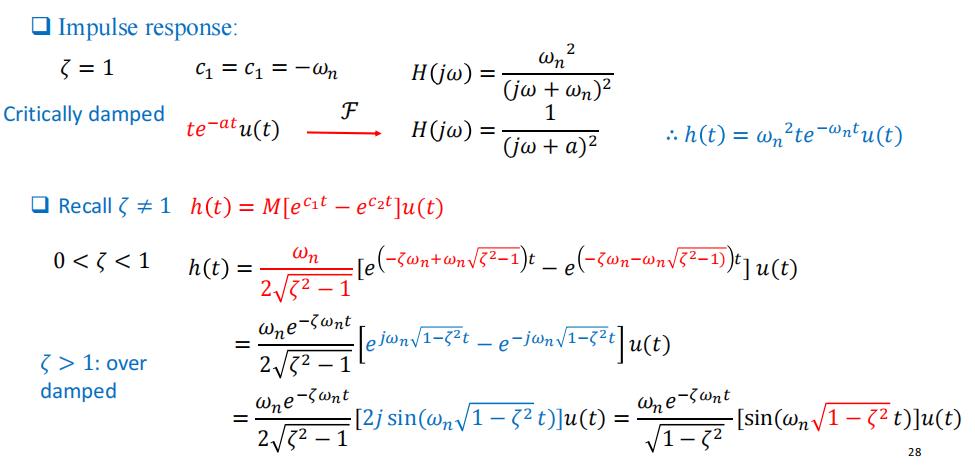
信号的采样与恢复
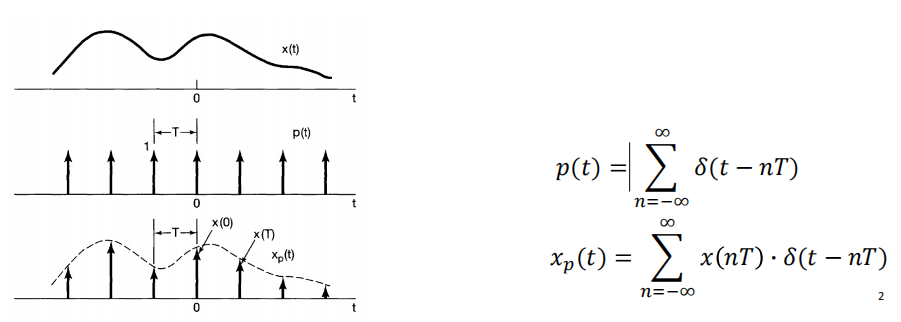
上图就是用一个离散的周期信号去采样$x(t)$的过程
但若$x(t)$是一个非周期的又带限的信号
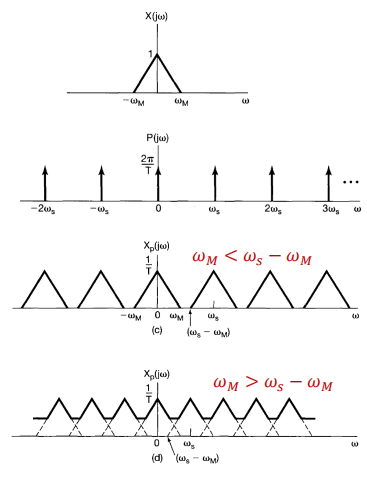
$X_p(jw)=\frac{1}{2\pi}X(jw)*P(jw)$
$P(jw)=\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(w-kw_s)=\frac{2\pi}{T} \sum_{k=-\infty}^{\infty} \delta(w-k\frac{2\pi}{T})$
$X_p(jw)=\frac{1}{2\pi}\sum_{k=-\infty}^{\infty}X(j(w-kw_s))$
观察得知,当$w_m<w_s+w_m$时候,信号采样的hi和不会出现重叠,若$w_m>w_s-w_m$信号会重复被采样,故部分信号缺失造成误差
故对有带限的信号,采样频率要满足$w_s>2w_m$这也就是采样定理
零阶保持

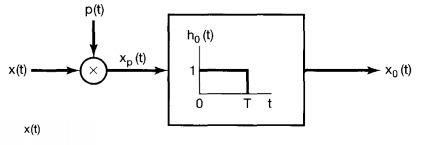
这是一种采样后恢复的方式
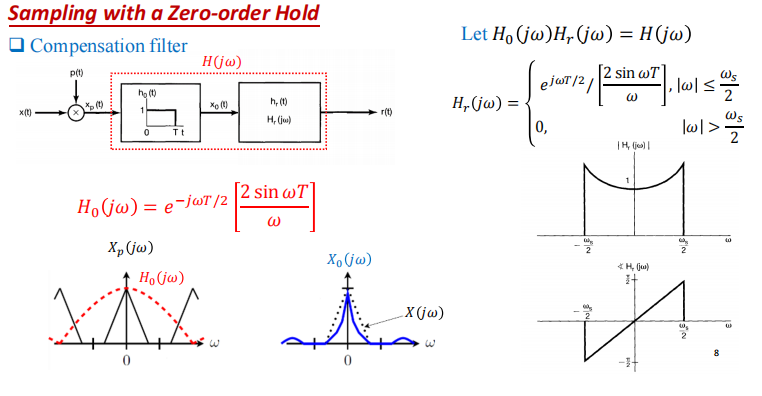
理想低通滤波器
$h(t)=\frac{Tw_c}{\pi} \frac{sinw_ct}{w_ct}$
$x_r(t)=\sum_{n=-\infty}^{\infty}x(nT)\frac{Tw_c}{\pi} \frac{sinw_c(t-nT)}{w_c(t-nT)}$
一阶保持
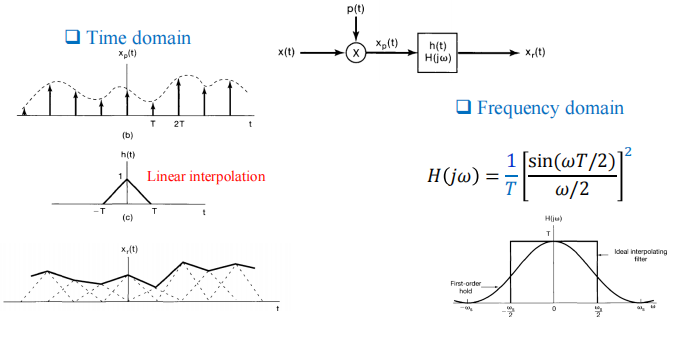
$H(jw)=\frac{1}{T}[\frac{sin(wT/2)}{w/2}]^2$
混叠(Aliasing)
当$w_s<2w_m$时,取样后会出现混叠现象
离散与连续时间信号转化
C/D conversion
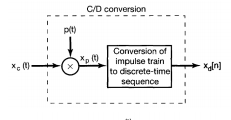
$x_p(t)=\sum_{n=-\infty}^{\infty}x(nT)\delta(t-nT)$
$x_d[n]=x_c(nT)$
推理过程:
$X_d(e^{j\Omega})=\sum_{-\infty}^{\infty}x_d[n]e^{-jn\Omega}=\sum_{-\infty}^{\infty}x_c(nT)e^{-jn\Omega}$
$x_p(t)=\sum_{n=-\infty}^{\infty}x_c(nT)\delta(t-nT) \rightarrow X_p(jw)=\sum_{n=-\infty}^{\infty}x_c(nT)e^{-jwnT}$
如果$w=\Omega /T,X_d(e^{j\Omega})=X_p(j\Omega/T)$
$X_d(e^{j\Omega})=1/T\sum_{k=-\infty}^{\infty}X(j(\Omega-2k\pi)/T)$
D/C conversion
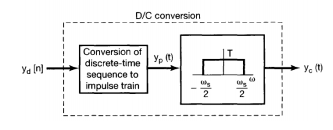
$y_c(t)=y[n/T]$
全系统
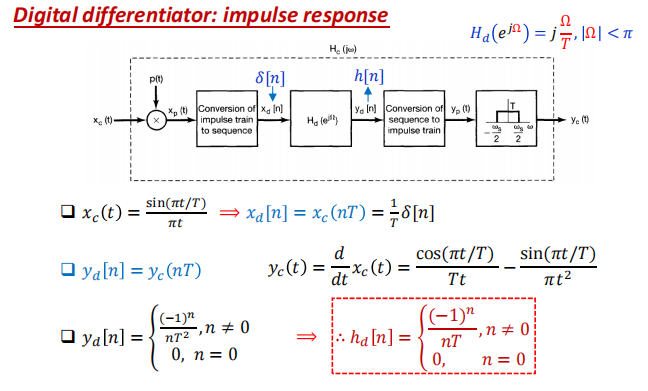
离散信号的采样
$X_p(e^{jw})=1/N\sum_{k=0}^{N-1}X(e^{j(w-kw_s)})$
离散信号的恢复
$x_r[n]=\sum_{k=-\infty}^{\infty}x[kN]\frac{Nw_c}{\pi}\frac{sinw_c(n-kN)}{w_c(n-kN)}$
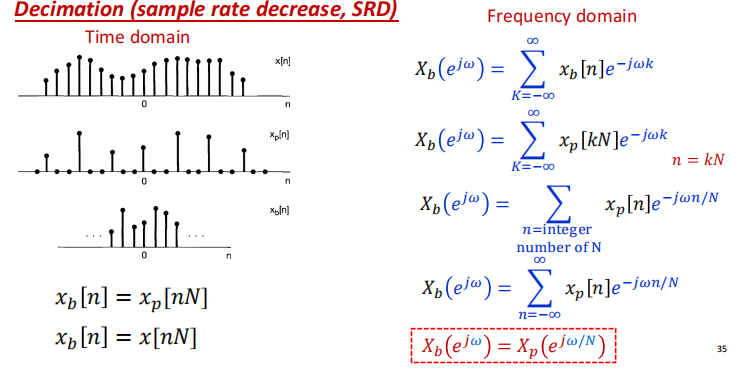
向下取样(SRI)因子M: $y[n]=x[Mn]$
拉普拉斯变换(The Laplace transform)
定义
傅里叶变换的拓展版
$x(t)\rightarrow X(s),X(s)=\int_{-\infty}^{\infty}x(t)e^{-st}dt,s=\sigma +jw$
当$s=jw$,就是傅里叶变换
定义域,零点,极点
这个是拉普拉斯变换区别于傅里叶变换特有的
定义域主要是看s的实部取值范围记为$Re[s]$
$X(s)=\frac{N(s)}{D(s)}$零点就是分子等于零时候s取值,极点是分母等于0的时候s取值
定义域一定不包括极点,零点无所谓
基本性质
The ROC of 𝑋 𝑠 consists of strips parallel to the 𝑗𝜔‐axis in the 𝑠‐p
$\int_{-\infty}^{\infty}|x(t)|e^{\sigma t}dt<\infty$ 用绝对可积来求定义域
For rational Laplace transforms, the ROC does not contain any poles.极点一定不在定义域之内
- If $x(t)$is of finite duration and is absolutely integrable, then the ROC is the entire s-plane.绝对可积则包含整个s平面
- 后面关于ROC和极点的性质不多赘述
反拉普拉斯变换
根据$X(s)$求$x(t)$
$x(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty}X(s)e^{st}ds$
图像性质

常用性质
线性:$x(t)=ax_1(t)+bx_2(t)\rightarrow aX_1(s)+bX_2(s),ROC :R_1 \and R_2$
时间平移:$x(t-t_0)\rightarrow e^{-st_0}X(s),ROC:R$
$X(s-s_0)\rightarrow e^{jw_0t}x(t),ROC:R$
翻倍:$x(at)\rightarrow \frac{1}{|a|}X(\frac{s}{a}),ROC:aR$
共轭:$x^(t)\rightarrow X^(s^*),ROC:R$
卷积:$x_1(t)*x_2(t)\rightarrow X_1(s)X_2(s),ROC:R_1\and R_2$
求导:$\frac{dx(t)}{dt}\rightarrow sX(s),ROC$ :contains $R$
$-tx(t)\rightarrow \frac{dX(s)}{ds}$
积分:$\int_{-\infty}^tx(\tau)d\tau \rightarrow \frac{1}{s}X(s),ROC:R\and [Re[s]>0]$
Initial‐value theorem:$x(0^+)= \lim_{s \rightarrow \infty}sX(s) $
Final‐value theorem:$\lim_{t \rightarrow \infty}x(t)=\lim_{s \rightarrow0}sX(s)$
特性
因果性(Causality):定义域包括右半平面
反因果性(Anti‐causal):定义域包括左半平面
稳定性(Stability):$H(s)$的脉冲响应绝对可积,定义域包括整个$jw$轴,即虚轴
对于因果系统,所有极点都在左半平面,即所有极点都有负实部
经典例题


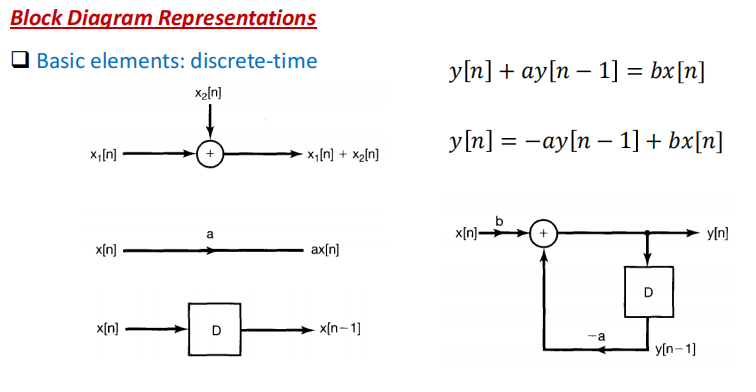
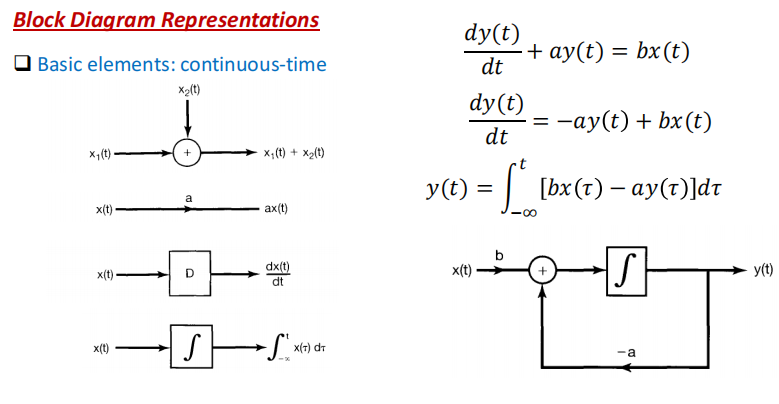
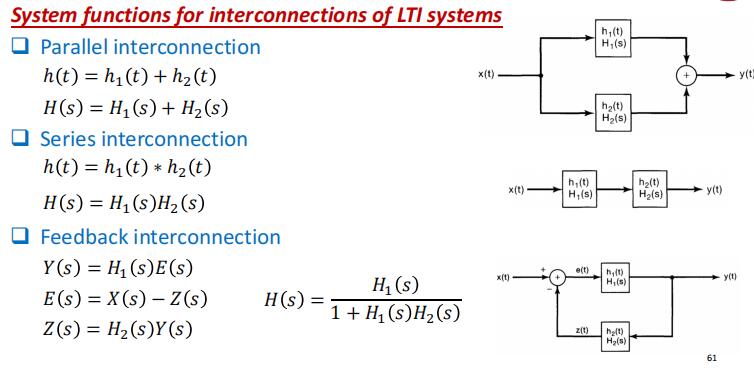
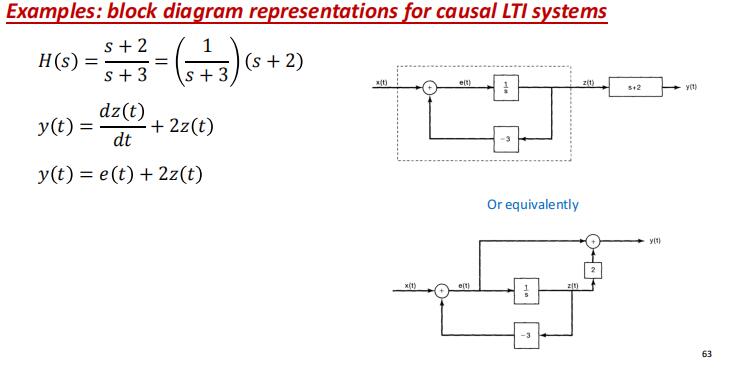
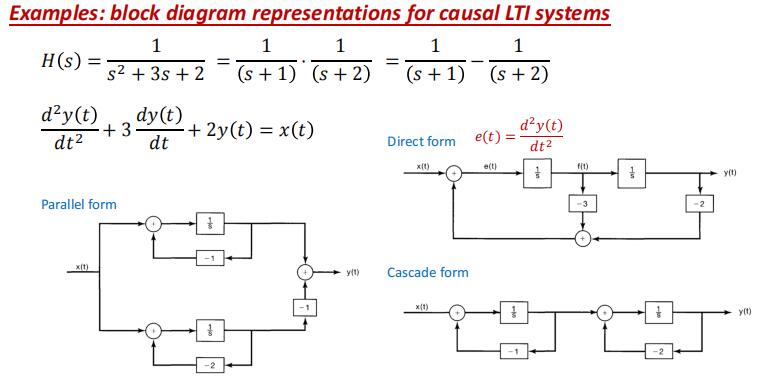
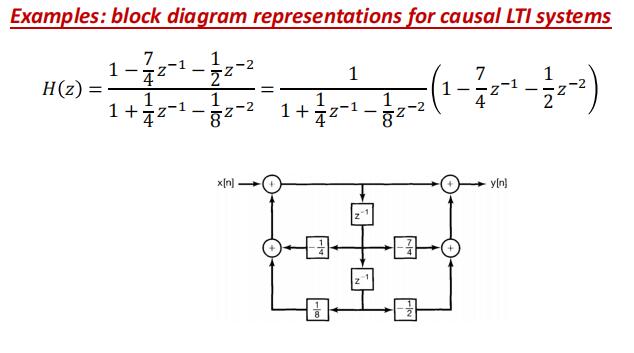
框图表示(Block Diagram Representation)
一阶系统
二阶系统的三种表示
如何看八爪鱼
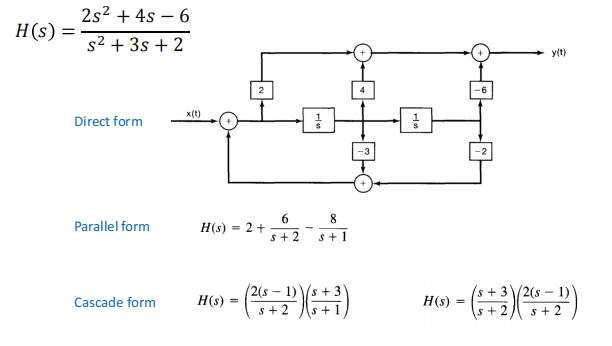
上面系数直接写,从幂高到低,下面系数取反。系数也是高到低写,没有框就是1
单边拉普拉斯变换
$X(s)= \int_{0^-}^{\infty}x(t)e^{-st}dt$
$x(t)=0$ for $t<0$ the unilateral and bilateral transforms are identical
不同的性质点
- 求导:$\frac{dx(t)}{dt}\rightarrow sX(s)-x(0^-)$
- 卷积:$x_1(t)*x_2(t)\rightarrow X_1(s)X_2(s),ROC:R_1\and R_2$只有$x_1(t),x_2(t)$都满足$t<0,x_1(t)=0,x_2(t)=0$才能用
用处:求LTI系统的零输入响应,和零状态响应

Z变换(The z‐transform)
定义
拉普拉斯变换的离散信号版本
$X(z)=\sum_{n=-\infty}^{+\infty}x[n]z^{-n}$
定义域都是圆型的
相似性质都和拉普拉斯相同不多赘述
反Z变换
$x[n]=\frac{1}{2\pi j}\int X(z)z^{n-1}dz$
注意定义域范围来确定最后得到函数
图像性质
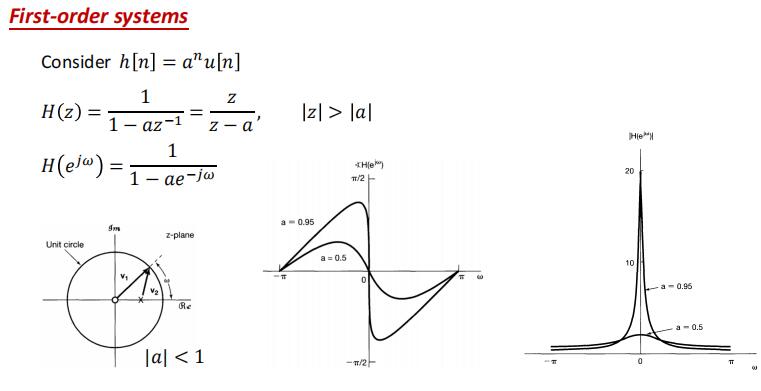
常用性质
线性:$ax_1[n]+bx_2[n]\rightarrow aX_1(z)+bX_2(z),ROC:R_1 \and R_2$
时间平移:$x[n-n_0]\rightarrow z_{-n_0}X(z),ROC:R$
$X(e^{-jw_0}z)\rightarrow e^{jw_0n}x[n],ROC:R$
共轭:$x^[n]\rightarrow X^(z^*),ROC:R$
求导:$nx[n]\rightarrow -z\frac{dX(z)}{dz},ROC:R$
$x[n]-x[n-1]\rightarrow (1-z^{-1})X(z),ROC :R$,
$\sum_{k=-\infty}^{n}x[k]\rightarrow \frac{1}{1-z^{-1}}X(z)$
特性
因果性(Causality):定义域在某个圆的外侧,包括无穷,$H(z)$分子的最高次数不能高于分母的最高次数
稳定性(Stability):定义域包含单位圆
如果系统因果,所有极点都在单位圆里面
经典例题:

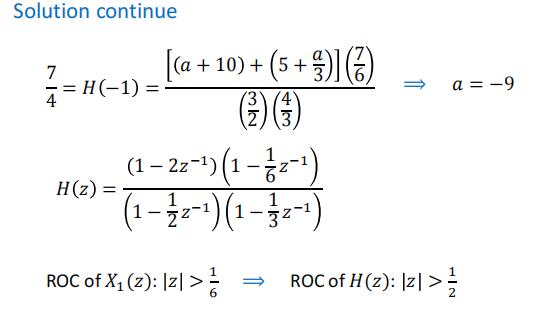

框图表示(Block Diagram Representation)
异曲同工
一阶系统
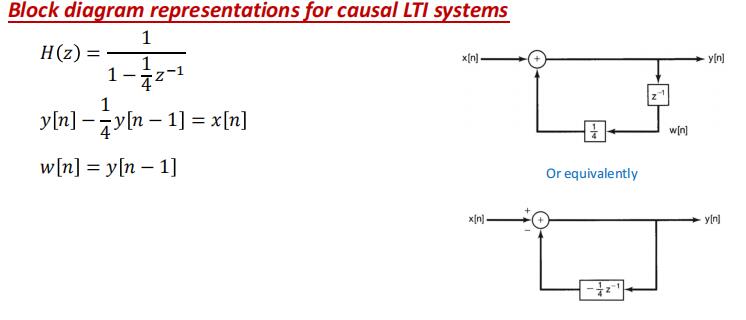
二阶系统
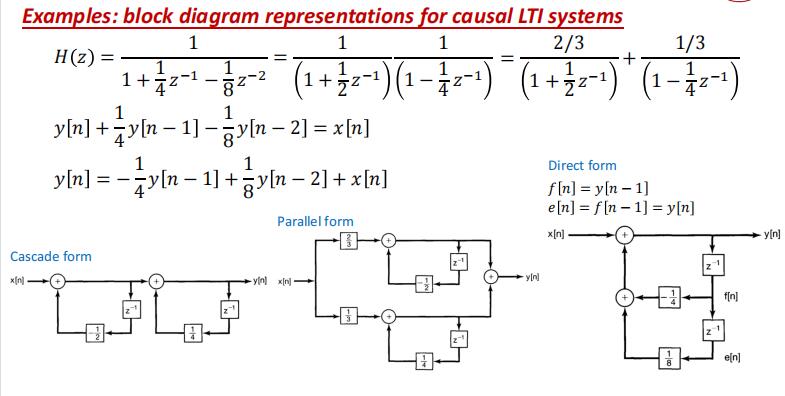
八爪鱼
单边Z变换
$X(z)=\sum_{n=0}^{\infty}x[n]z^{-n}$
特殊性质
- $x[n+1]\rightarrow zX(z)-zx[0]$
- $x[n-1]\rightarrow z^{-1}X(z)+x[-1]$
- $x[n-2]\rightarrow z^{-2}X(z)+z^{-1}x[-1]+x[-2]$
主要和单边拉普拉斯变换有相同用处
