参考博客:背包 N,NP,NPC A*这几个比较难所有参考比较多
基本概念
Poly-time: There exists constants $c > 0$ and $d > 0 $such that on every input of size N, its running time is bounded by $cN^d$ steps
基础结构
链表(List)
记录头尾指针代表链表的开始和结束,中间用next表示前后关系的线性结构。
支持的操作与其复杂度
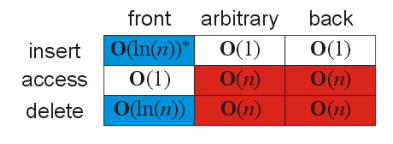
· 头尾插入元素$O(1)$,删除尾部$O(n)$
· 其他位置插入删除都是$O(n)$(先要找到这个元素再在前后插入,知道位置只用$O(1)$)
双向链表就是多记录了一个$pre$,没啥大区别
栈(Stack)
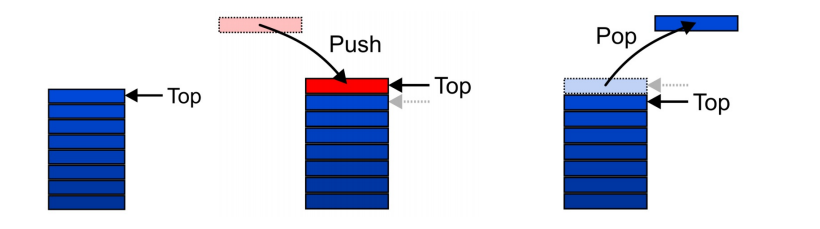
尾进尾出的结构,一般只需要一个指针,画成竖直状态比较方便理解
具体运用:逆波兰表达式,树的深度优先遍历
队列(Queue)
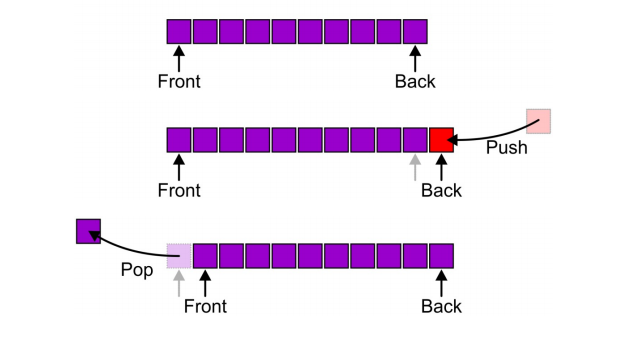
尾进头出的结构,有头尾两个指针的线性结构
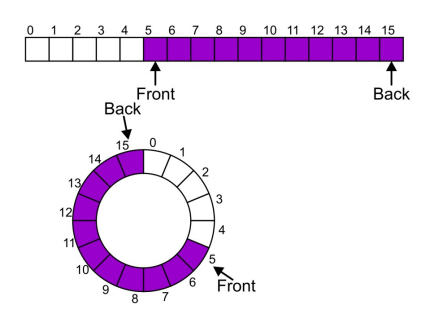
环形队列
哈希表(Hash List)
自定义一种哈希方式,得到对应的哈希数,然后放在对应的数组格子里面。
但如果对应格子已经满了,就采用线性或者更跳跃的方式往后找空余的格子
线性探查(probe)——直接一个一个往后找
二次探查——$ (k+k*k)/2$ 1,2,4,7,11 优点为花费时间更少
树(Trees)
基本概念
- 深度(depth):根节点记为深度0,树的高度指最大深度
- 父亲(parent)与孩子(children)节点:从根节点往下遍历,由一条边相连的两个节点互为父亲与孩子节点,深度小的为父亲
- 度数(degree):父亲节点的孩子数量
- 叶子节点(leaf):孩子数量为0即度数为0的节点
- 根节点(root):没有父亲的节点
- 祖先(ancestor)与子孙(descendant):此概念均包括节点自己,子孙指以该节点为根的子树里所有的节点,祖先指从该节点到根节点路径上经过的所有节点
遍历方法(traversal)
广度优先遍历(Breadth-First Traversal) BFS
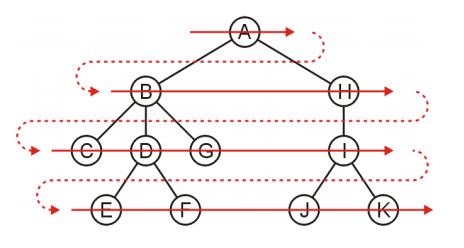
很显然的遍历,运用queue队列来进行,每次先pop对头节点,再push进去当前 对头节点所
有的孩子
深度优先搜索(Depth-first Traversal) DFS
每次pop出栈头节点,push进去其孩子节点(从右到左)
用栈stack来实现
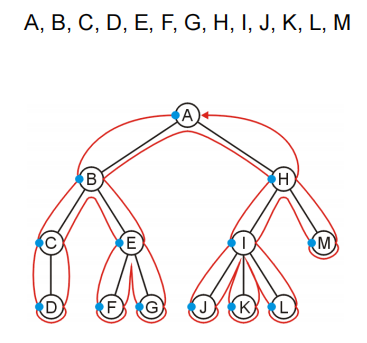
二叉树(Binary Tree)
一种孩子最多只有两个的结构
二叉树的深度遍历
- 前序遍历(pre-order):根左右
- 中序遍历(in-order):左根右
- 后序遍历(post-order):左右根
都是以根的位置而记忆的
易混淆概念
- 满二叉树(full binary tree):只要有孩子就必须满足两个,要么就没有
性质:$n $ 个叶子节点,$2n-1$ 所有节点
完美二叉树(perfect binary tree):每层的节点全部是满的
性质:节点为$n=2^{h+1}-1$,高度为$h=\Theta(lnn)$,该层有$2^h$个叶子节点
完全二叉树(complete binary tree):倒数第二层前都满足完美二叉树性质,最后一层可以不满
性质:节点为n,高度为$h=\lfloor lg(n) \rfloor$
复杂度计算
三种复杂度表示的定义和证明
• Upper bounds. T(n) is $ O(f(n))$ if there exist constants c > 0 and $n_0 \geq 0$ such that for all $n \geq n_0$we have$ T(n) \leq c・f(n)$
• Lower bounds. T(n) is $Ω(f(n))$ if there exist constants $ c > 0 $and $ n_0 \geq 0 $such that for all $n \geq n_0$ we have $T(n) \geq c・f(n)$
• Tight bounds. T(n) is $ Θ(f(n))$ if T(n) is both $ O(f(n))$ and $ Ω(f(n))$.
• Exist constants$ c_1, c_2, n_0$, such that$ c_1f(n) \leq T(n) \leq c_2f(n) $for all$ n \geq n_0$
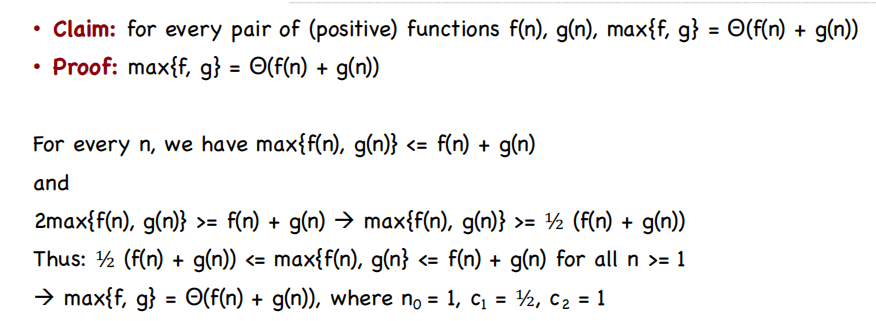
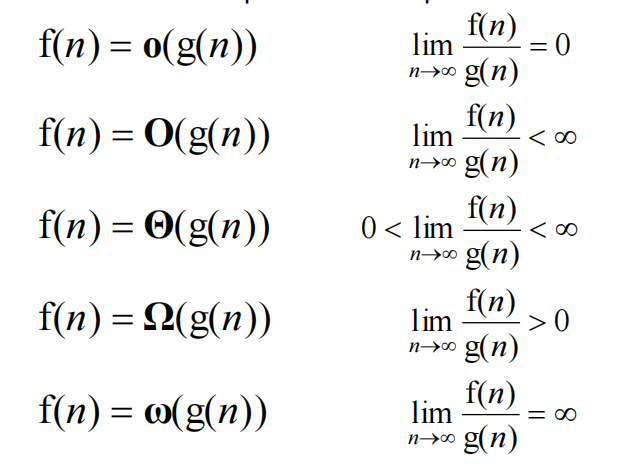
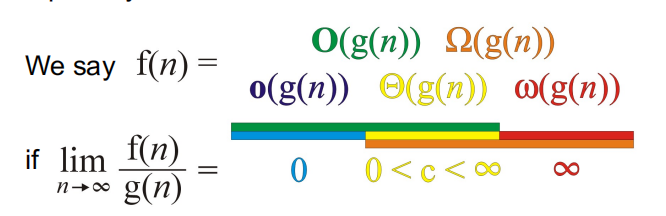
关于复杂度的加法原则

多项式的一些复杂度定理:
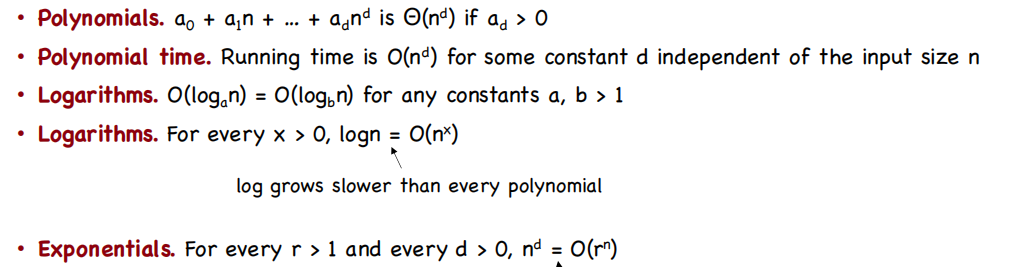
$O(k^2n^k/k!)=O(n^k)$
数据结构相关算法
排序算法
逆序对定义:原先数组内和排序后数组顺序相反的数对
计算逆序对:用归并排序
插入排序(Insertion Sort)
将序列分为有序序列和无序序列两段,每次将无序序列开头的数插入前面的有序序列中,直到所有数都有序
复杂度:最坏$O(n^2)$,平均$O(n+d)$,原地排序,稳定排序
若有$d$对逆序对,则时间为$\Theta (n+d)$
若$d=O(n)$,时间为$\Theta(n)$
冒泡排序(Bubble Sort)
从前到后比较相邻两个数的大小,交换逆序对
同时分带不带flag判断,带的话有最优复杂度,不带就没有
复杂度:最坏$O(n^2)$ 最优$O(n)$ ,原地排序,稳定排序
归并排序(Merge Sort)
归并思路,合并两个子数列的时候就是利用队列合并,所以需要新开一个数组来合并序列
复杂度:$O(nlogn)$ 非原地排序,空间$O(n)$,稳定排序
计算逆序对,直接在$b_j<a_i$时候$ans+=mid-i+1$
快速排序(Quick Sort)
每次选一个pivot找到他正确的位置,然后以pivot为中心再分为两个子序列,于是剩下的就是分治思路。
找位置的方法是,从pivot开始从左到右找第一个比pivot大的数,从右到左找第一个比pivot小的数
同时每次把pivot找到的正确位置之后,就是建立一颗二叉搜索树。
从这个角度思考复杂度$a_i,a_j$会被比较到的概率为$2/j-i+1$,只有互为孩子父亲才会被比较到
故复杂度就为所有数对的可能性相加 $2n(lnn+1)$
复杂度:平均$O(nlogn)$ 最坏$O(n^2)$,原地排序,非稳定排序
堆排序(Heap Sort)
先把数据建成大根堆,每次再将堆头和最末尾的元素交换,然后pop掉这个最大的元素,再重新调成大根堆结构,这样保证每次操作都能找到现在无序序列中最大的元素,依次把大根堆规模变小,使无序序列长度逐渐变小为0。
复杂度:$O(nlogn)$,非原地排序,非稳定排序
选择排序(Selection Sort)
每次从前往后找出无序序列中最小的一个数和无序序列第一个数交换位置,暴力找,很慢。
复杂度:$O(n^2)$,原地排序,非稳定排序
Master Theorem
一个在归并算法中运用的求复杂度的理论
$
T(n)=aT(\frac{n}{b})+f(n),T(0)=0,T(1)=\Theta(1)
$
a代表子问题的数量,n/b指子问题的大小,f(n)是divide and combine
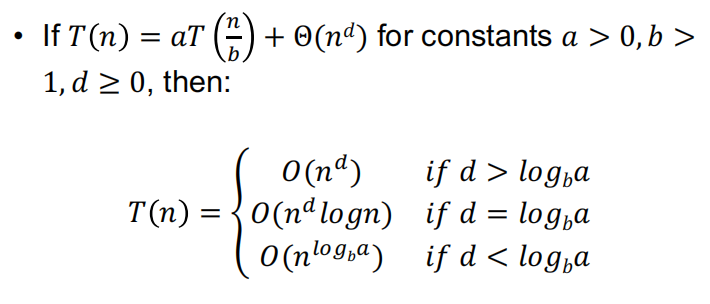
这个理论运用的实例:求矩阵乘法

哈夫曼编码(Huffman Coding)
一种按字符出现频率来实现编码的方式,以此来节省空间,利用二叉树,优先队列来存储
先用优先队列记录每个字符的出现频率,频率越高在优先队列中优先级越低,就放在队列越后面
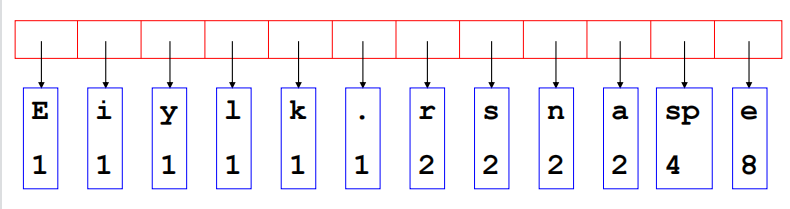
建树过程使从前到后两两合并,得到的子树顺次插入序列,期中单字符优先级大于多个字符
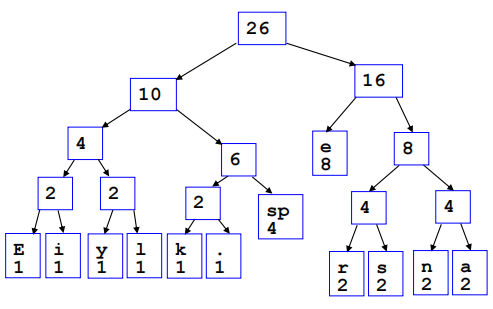
二叉堆与优先队列(Heap)
优先队列就是队头固定最大最小值的数组,感觉就是排好序的数列
二叉堆的性质:大根堆就是父亲节点大于左右孩子,但左右孩子大小关系不确定,小根堆就是大小关系反一下
堆是一个完全二叉树,将数据储存在数组里的,利用下标一个父亲节点为$n$则左孩子为$2n$,右孩子$2n+1$
操作与复杂度
push:直接先新节点顺次加入树的最后一个节点,然后执行percolate操作,我的理解是向上翻,每次比较第$\lceil n/2 \rceil(n>>1)$节点和自己的大小,若不符合定义就交换。
pop:将需要pop的节点与当前堆最后一个元素交换,直接抛弃现在最后一个元,再执行percolate操作,在这里是下沉,再从根节点往下比较自己孩子$(2n,2n+1)$与自己的大小,不符合定义就交换。
build:push每个元素或者用Floyd’s Method $O(nlogn)$
大体看push和pop都当成$O(nlogn)$
空间都是$O(n)$
Floyd’s Method将小根堆调成为大根堆(或者将普通堆调整),就是思路是先从上往下找到所有不符合定义的根节点,从编号最大的节点依次往上做percolate操作调成,依次调整完就行。
斐波那契堆(Fibonacci Heap)
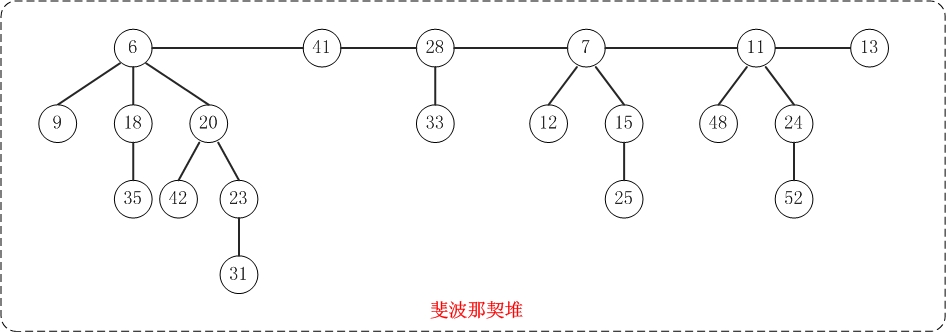
$FibNode$是斐波那契堆的节点类,它包含的信息较多。$key$是用于比较节点大小的,$degree$是记录节点的度,$left$和$right$分别是指向节点的左右兄弟,$child$是节点的第一个孩子,$parent$是节点的父节点,$marked$是记录该节点是否被删除第1个孩子($marked$在删除节点时有用)。
$FibHeap$是斐波那契堆对应的类。$min$是保存当前堆的最小节点,$keyNum$用于记录堆中节点的总数,$maxDegree$用于记录堆中最大度,而$cons$在删除节点时来暂时保存堆数据的临时空间。
不具体介绍每部操作如何实现教学指路
| 过程 | 二叉堆 | 斐波那契堆 |
|---|---|---|
| INSERT | $O(logn)$ | $O(1)$ |
| MINIMUM | $O(logn)$ | $O(1)$ |
| UNION | $O(logn)$ | $O(1)$ |
| DELETE | $O(logn)$ | $O(logn)$ |
二叉搜索树(Binary Search Trees)
满足根节点的左子树所有值都小于自己,右子树所有值都大于自己的二叉数
理解:$BST$的结构主要和插入元素的顺序有关,优不优化完全取决顺序,所以才有了$AVL$树
操作与复杂度
- Insert:总的来说就是顺着根节点往下比较,每次看是比当前节点大还是小,小就往左边走,大就往右边走,知道找到一个空位置就行
- Find:和插入同理,顺着树往下走就完了
- Erase:这个分三种情况,若该节点为叶子节点直接删除就行,如果有一个子树,把这个子树接上去就行,如果有两个子树,找到右子树中最小的元素和根换位置再删掉根就行,这样能保证现在右子树所有值还是大于根(最小元素),左子树所有值也小于根。同时这个最小的值一定只有一个子树或者右节点可以证明,因为使最小的不可能有左子树
由于所有操作都等于$O(h)$,但高度决定于顺序所以没有定值,但最优$O(lognn)$,最坏$O(n)$
一些进阶设计
设计$next$边:如果该节点有右子树,根向右子树最小的值连next边
设计$previous$边:如果该节点没有右子树,找到第一个大于自己的节点向他连一条边
这个课件里没有讲有啥用,我感觉就和AC自动机一样,但不知道有啥实际运用
感觉是next在删除中比较有用吧
用$BST$找第k大:直接看根节点左右子树大小,若左子树大小$l=k$,就是root。若$l>k$继续在左子树中找最大的,否则在右子树中找$k-l-1$大的,就是一个递归思路
二叉平衡搜索树(AVL Trees)
就你是我以前天天写到吐的玩意是吧!
就是$BST$升级版,需要保证左右子树高度差距不大于1,于是所有操作的复杂度就能在$O(logn)$了
完全二叉搜索树=平衡树
计算满足高度为h的最小平衡树$F(h)$:可得此为斐波那契数列
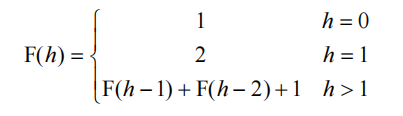
得到$F(h)\approx 1.8994\phi ^h-1,\phi \approx 1.6180$
$F(h)=\Theta (\phi ^h)$
所以可得高度为h的最大平衡树$log_{\phi}{(\frac{n+1}{1.8944})}=log_{\phi}{(n+1)-1.3277}=1.4404*lg(n+1)-1.3277$
操作与复杂度
所有操作和$BST$一样,只是插入和删除都多了一个维和操作,这里具体分析如何维护也就是$Splay$核心,同时维护都是$O(1)$
基本操作分为左旋和右旋
右旋
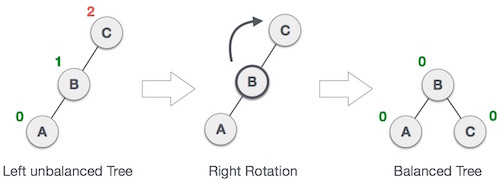
左旋
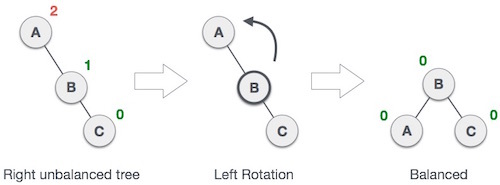
核心是找到处于不平衡状态的根,看是怎么样子不平衡
LL
左子树大于右子树两个高度,直接右旋一次就行
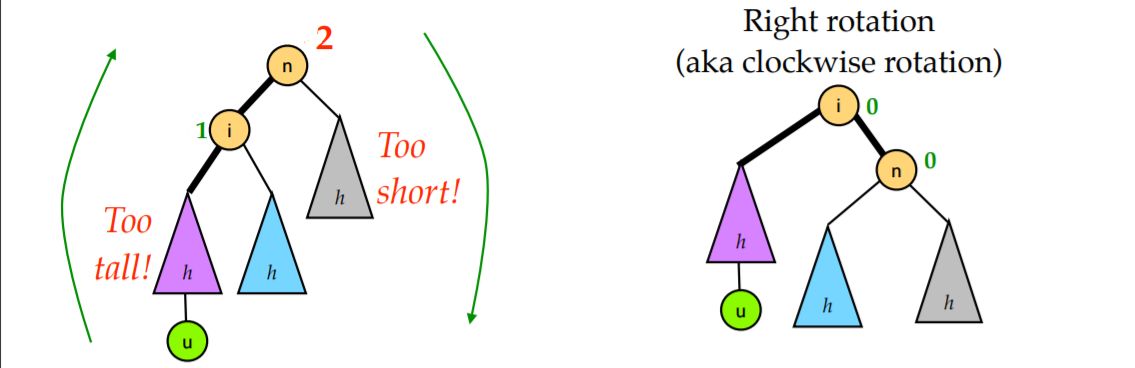
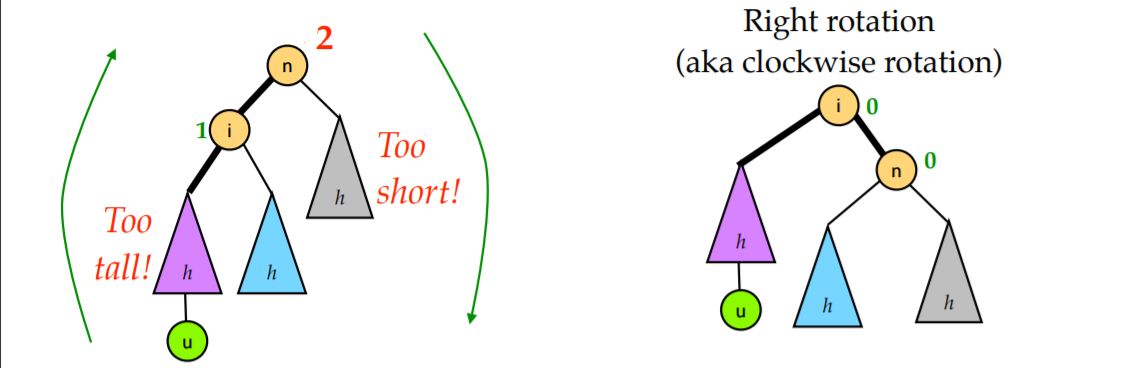
RR
右子树大于左子树两个高度,直接左旋一次就行
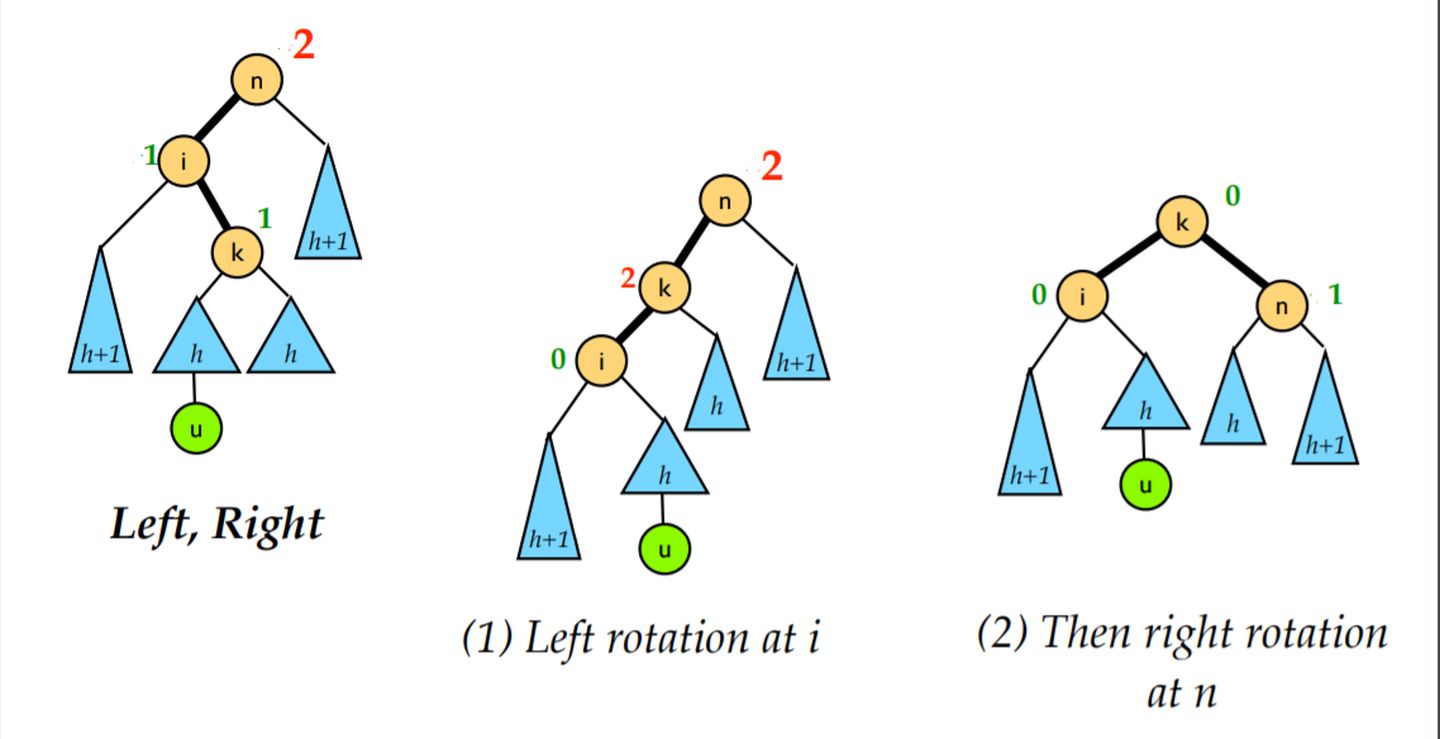
LR
将新的节点插入到了 n 的左孩子的右子树上导致的不平衡的情况。这时我们需要的是先对 i 进行一次左旋再对 n 进行一次右旋。
RL
和LR同理不知道为啥没有图给我偷了(
总之是将新的节点插入到了 n 的右孩子的左子树上导致的不平衡的情况。这时我们需要的是先对 i 进行一次右旋再对 n 进行一次左旋。
再来看基本操作
- Insertion 只可能需要一次维护 $O(1)$
- Erase 可能需要$O(h)$次数,需要沿着删除的节点从下到上沿着到根节点的路径往上检查节点是否需要为维护 故复杂度$O(log n)$
并查集(Disjoint Set)
主要操作
主要操作是$findf()$和$union$,每次$union就是把两个节点接到一颗树上,findf就是找到这个节点对应的根节点。
关于这个add的方式主要分为两种
例子$union(A,B),root(A)=C,root(B)=D$
1.Only with path compression
指只看前后顺序来merge,把D接在C下面
2、Only with union-by-size optimization(又称rank优化)
指当两颗子树高度一直时按前后顺序加,若不同就把高度更低的加到高度高的树根下面
如果$height(C)>height(D)$,把D接在C下面,否则和1相同
还有一种size优化,是比较每颗子树的size来合并,但没有rank好
一般写代码会用到路径压缩的方式,即所有子树高度都压缩到1,就是最常见的写法。
int findf(int x)
{
if(fa[x]==x)return x;
else return fa[x]=findf(fa[x]);
}
void dij_add(int x,int y)
{
int fx=findf(x);
int fy=findf(y);
if(fx==fy)return ;
fa[fx]=fy;
}
若不使用路径压缩,我们通过并查集得到的树有一下结论。

假如这颗树高度为$h$,有节点数$\sum_{k=0}^{h}\dbinom{h}{k}=2^h=n$
深度$\sum_{k=0}^{h}k\dbinom{h}{k}=h2^{h-1}$
平均深度$\frac{h2^{h-1}}{2^h}=\frac{h}{2}=\frac{lg(n)}{2}$
时间复杂度
$findf$:优化前$O(n)$,rank优化+路径压缩后$O(log^*n)$
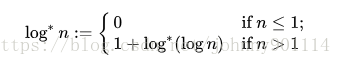
| n | log* n |
|---|---|
| (−∞, 1] | 0 |
| (1, 2] | 1 |
| (2, 4] | 2 |
| (4, 16] | 3 |
| (16, 65536] | 4 |
| (65536, 2^65536] | 5 |
总之这个$log^*n$优于$logn$
以上为数据结构的相关算法,接下来是图论。
图论
基础概念
- 有向图(Directed graph):点之间的边指定方向。如由A→B最大边数$|E|\le O(2|V|^2)=O(|V|^2)$
- 无向图(Undirected graph):点之间的边不指定方向。最大边数$|E|\le O(|V|^2)$
- 度(Degree): 出度(Out)入度(In)针对有向图,计数从一个点出去的边数和接受的边数。对于无向图就是一个点连了多少条边
- 子图(Sub-graph):从原图中选取部分边和点
- 顶点导出子图(Vertex-induced sub-graphs):所有的点都选,边部分不选
- 路径(Path):两点之间遍历到的点集合
- 最简路径(Simple path):点边不可重复走
- 最简回路(Simple cycle):(除去头尾)点边不可重复走的环
- 联通(Connectedness):两点之间存在路径则联通
- 树(Tree):每两点间都只有一条独立的路径
- 森林(Forest):没有任何回路的图,树的合集
- 联通分量(Connected Components):连通的子图
储存方式
邻接矩阵(Adjacency Matrix):空间$O(|V|^2)$,遍历所有邻接的点$\Theta(|V|)$
邻接表(Adjacency List):空间$\Theta (|V|+|E|)$,遍历所有邻接的点$\Theta(|E|/|V|)$ 更适合于
图的遍历
- 深度优先搜索(用栈):递归或者栈,一次性一条路走到底,若到底则返回遍历,继续往下找
- 广度优先搜索(用队列)每次push进去邻接的点,pop出去的点就是遍历顺序
两种遍历都可以检查图的联通性
关于二分图:
如果某个图为二分图,那么它至少有两个顶点,且其所有回路的长度均为偶数,任何无回路的的图均是二分图。
算法判定:用二分图染色
算法
最小生成树(Minimum Spanning Tree)
总之是求图上构造一棵树是所有点连通,并且边的权值之和最小。
默认是邻接矩阵实现
prim算法
- 首先初始化距离为INF
- 随机从一个点开始,先遍历他邻接的点更新一下初始距离,再遍历所有的点找到一个距离最短的点,并记录下来 $O(|V|^2)$,相当于pop小根堆堆顶的点
- 再从这个点开始遍历邻接所有的点,更新距离$O(|E|)$,相当于加入小根堆
- 直到遍历到所有点
此算法需要储存邻接的边信息,比如需要前向星
故总的时间复杂度$O(|V|^2+|E|)=O(|V|^2)$
用邻接表$O(|V|ln|V|+|E|ln|V|)=O(|E|ln|V|)$
斐波那契堆$O(|V|ln|V|+|E|)$二叉堆$O(|V|ln|V|+|E|ln|V|)=O(|E|ln|V|)$
Kruskal算法
- 先将边按照权值排序(从小到大)$O(ln|E|)$
- 遍历所有的边,对于每条边的连接的两点$u,v$,对其进行一次并查集的判断,看这两个点是否联通,如果联通则放弃,不连通则加入生成树$O(|E|ln|V|)$
复杂度$O(ln|E|+|E|ln|V|)=O(|E|ln|V|)$
不需要前向星只需要结构体
拓扑排序
就是根据图上每个点的入度来排序的算法,每次找到所有点中入度为0的点,将其pop出队列,然后将这个点所邻接的点的入度–,更新后重新寻找入度为0的点。
一些结论:
- DAG一定有拓扑排序,有拓扑排序一定是DAG(有向无环图)
- DAG一定至少有一个入度为0的点
- DAG的子图一定是DAG
- 不是DAG一定没有拓扑排序
复杂度:
$O(|V|+|V|^2)=O(|V|^2)$不使用堆,每次遍历所有的点找入度为0的点
若使用堆优化$O(|V|+|E|)$邻接表,$O(|V|^2)$邻接矩阵
若某次操作后,所有剩下的点没有入度为0的点,则有环,因此可以用拓扑排序判环
用拓扑排序找critical path
总之描述是每个点带一个时间权值,当入度都为0的时候可以同时进行操作,求所有任务完成的最短时间和路径。
就用拓扑排序,每次记录一下前一个点是哪个就可以了,删除点的时候顺便更新邻接点的最短时间就可以了
最短路
声明:所有最短路算法遇到负环均没有答案
Dijkstra
方法是先将所有点的距离都赋值为INF,从起点开始,每次找到距离最短的点,从这个点来更新邻接的点的距离
$dis[u]=min(dis[u],dis[v]+w(u,v))$
注意:
- $dijkstra$不能计算有副边边权的最短路
- 有向图无向图都一样
复杂度:
邻接矩阵:$O(|V|(|V|+|V|))=O(|V|^2)$
邻接表:$O(|V|^2+|E|)=O(|V|^2)$
堆优化+邻接表:二叉堆 $O(|V|ln|V|+|E|ln|V|)=O(|E|ln|V|)$
斐波那契堆 $O(|V|ln|V|+|E|)$
Bellman-Ford
我认为十分垃圾的算法,总之唯一优点是可以处理负边
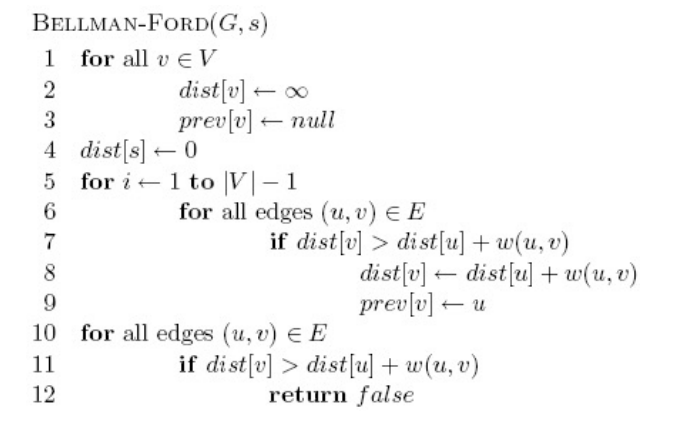
最后的循环是用来判断负环
复杂度:
$O(|V|+|V||E|)=O(|V||E|)$
Spfa
Bellman-Ford 的队列优化 和Dijkstra就是孪生兄弟
基本写法只有vis数组的更新以及堆和队列区别,一旦入队,vis变为1,出队就变为0,松弛的时候遇到不在队列里的点就进队,在队列里面就只是更新距离
Dijkstra是一旦出堆一次就不会再进去
//队列存的是待更新的点
queue⬅st
while(queue不空) {
Ⅰ.t=queue.front();//取出队首元素
q.pop();
Ⅱ.更新t的所有出边 t→b(权值为w)
//如果更新成功的话,就把b加入队列,b就是待更新的点,先判断b是否已经被更新过了,如果已经更新过了
}
一般情况下时间复杂度:$O ( |E| )$,最坏的情况下是:$O(|V||E|)$
Floyd
当$|E|=\Theta(|V|^2)$,用$Dijkstra$求所有点对的最短路$O(|V|^3ln|V|)$太拉了所以用Floyd
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
注意:如果是无向图,第二层只需要遍历$k+1-n$,时间节约约1/2
可以用Flody判断联通性以及负环,跑完后只要有负值就是负环
A*
在一些情况下,如果我们可以预先计算出每个节点到终点的距离,则我们可以利用这个信息更快的到达终点。
其原理也很简单。与Dijkstra算法类似,我们也使用一个优先队列,但此时以每个节点到达终点的距离作为优先级,每次始终选取到终点移动代价最小(离终点最近)的节点作为下一个遍历的节点。这种算法称之为最佳优先(Best First)算法。
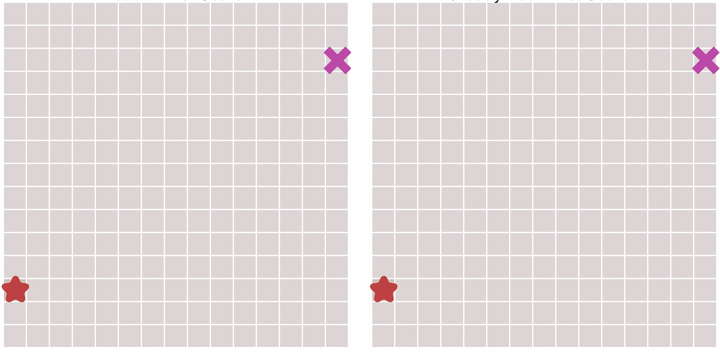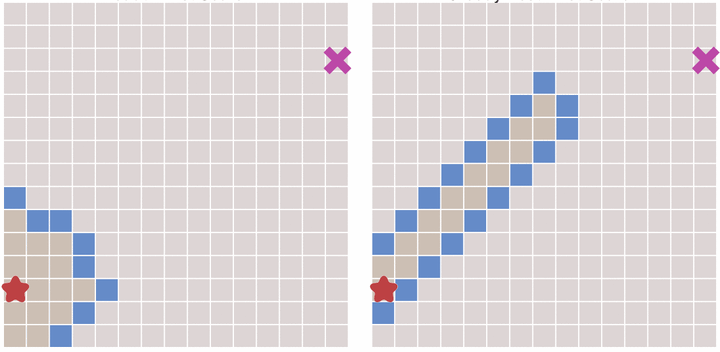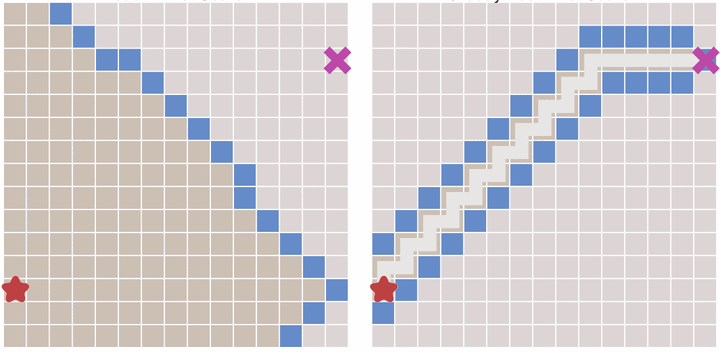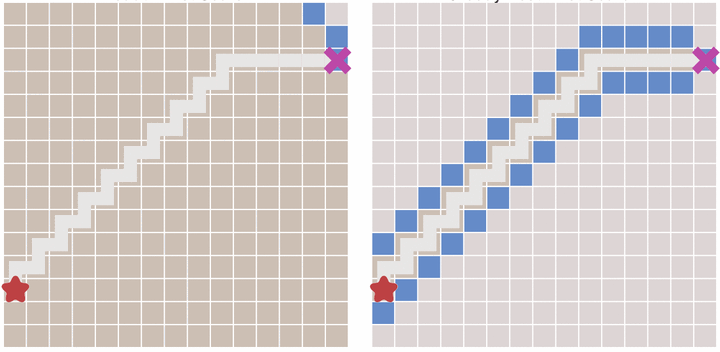
启发式搜索,为每个点添加一个优先级函数
A*算法通过下面这个函数来计算每个节点的优先级。
$f(n)=g(n)+h(n)$
其中:
- $f(n)$是节点n的综合优先级。当我们选择下一个要遍历的节点时,我们总会选取综合优先级最高(值最小)的节点。
- $g(n) $是节点n距离起点的代价。
- $h(n)$是节点n距离终点的预计代价,这也就是A*算法的启发函数。关于启发函数我们在下面详细讲解。
A*算法在运算过程中,每次从优先队列中选取$f(n)$值最小(优先级最高)的节点作为下一个待遍历的节点。
* 初始化open_set和close_set;
* 将起点加入open_set中,并设置优先级为0(优先级最高);
* 如果open_set不为空,则从open_set中选取优先级最高的节点n:
* 如果节点n为终点,则:
* 从终点开始逐步追踪parent节点,一直达到起点;
* 返回找到的结果路径,算法结束;
* 如果节点n不是终点,则:
* 将节点n从open_set中删除,并加入close_set中;
* 遍历节点n所有的邻近节点:
* 如果邻近节点m在close_set中,则:
* 跳过,选取下一个邻近节点
* 如果邻近节点m也不在open_set中,则:
* 设置节点m的parent为节点n
* 计算节点m的优先级
* 将节点m加入open_set中
close_set:储存出队的节点,open_set:目前队列,已$f(n)$为依据的小根堆,parent用来记录路径
一些结论:
- 在极端情况下,当启发函数$h(n)$始终为0,则将由$g(n)$决定节点的优先级,此时算法就退化成了$Dijkstra$算法。
- 如果$h(n)$始终小于等于节点n到终点的代价,则A*算法保证一定能够找到最短路径。但是当$h(n)$的值越小,算法将遍历越多的节点,也就导致算法越慢。
- 如果$h(n)$完全等于节点n到终点的代价,则A*算法将找到最佳路径,并且速度很快。可惜的是,并非所有场景下都能做到这一点。因为在没有达到终点之前,我们很难确切算出距离终点还有多远。
- 如果$h(n)$的值比节点n到终点的代价要大,则A*算法不能保证找到最短路径,不过此时会很快。
- 在另外一个极端情况下,如果$h(n)$相较于$g(n)$大很多,则此时只有h(n)产生效果,这也就变成了最佳优先搜索。
Tree Search:不设置vis数组,不考虑节点有无被遍历过
Graph Search:设置vis数组,每次出堆的时候就标记visited,每次只遍历邻接的unvisited的点
$h(n)$又称heuristic distance,关于这个距离有两个性质
- Admissible Heuristics,就是$h(n)$始终小于等于节点n到终点的代价
Theorem: If h(n) is admissible, A* using TREE-SEARCH is optimal
- Consistent Heuristics
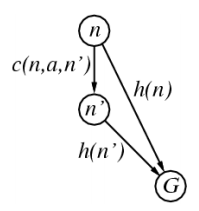
A heuristic is consistent if for every node n, every successor n’ of n
generated by any action a, we have h(n) ≤ c(n,a,n’) + h(n’)
If h is consistent, we have
f(n’) = g(n’) + h(n’) =g(n) + c(n,a,n’) + h(n’) (g(n’)=g(n)+c(n.a.n’))
≥ h(n) + h(n) = f(n) (consistency)
f(n’) ≥ f(n)
这个性质只针对两个点,基本就看$h(n),h(n’)+w(n,n’)$
Theorem: If h(n) is consistent, A* using GRAPH-SEARCH is optimal
其他算法
贪心
主要列举一下证明,反证法

Inversions
An inversion in schedule S is a pair of jobs i and j such that: i < j but j scheduled before i
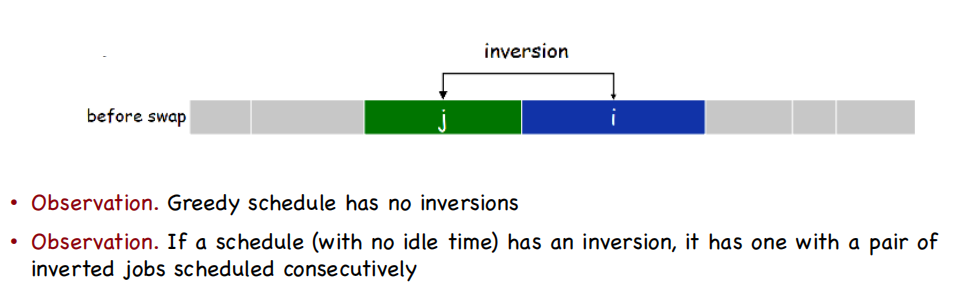
贪心没有inversions,inversions一定相邻
DP
这个就不说理论了,直接上例题
背包问题
01背包
$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]),j >= w[i]$
for(int i=1;i<=n;i++) for(int j=V;j>=w[i];j--) f[j]=max(f[j],f[j-w[i]]+val[i]);完全背包
$dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]]+v[i]) ,j >= w[i]$
for(int i=1;i<=n;i++) for(int j=w[i];j<=V;j++) f[j]=max(f[j],f[j-w[i]]+val[i]);多重背包
前面不同就是每种物品是有限个$n[i]$
$dp[i][j] = max{(dp[i-1][j − kw[i]] + kv[i]) for every k},k <= min(n[i], j/w[i])$
其他情形:
恰好装满:
背包问题有时候还有一个限制就是必须恰好装满背包,此时基本思路没有区别,只是在初始化的时候有所不同。
如果没有恰好装满背包的限制,我们将dp全部初始化成0就可以了。因为任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了。如果有恰好装满的限制,那只应该将$dp[0,1,..N][0]$初始为0,其它dp值均初始化为
-inf,因为此时只有容量为0的背包可以在什么也不装情况下被“恰好装满”,其它容量的背包初始均没有合法的解,应该被初始化为-inf。求方案数量:$dp[i][j] = sum(dp[i−1][j], dp[i][j−w[i]]) // j >= w[i]$
经典例题
- Partition Equal Subset Sum(分割等和子集)
题目给定一个只包含正整数的非空数组。问是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
由于所有元素的和sum已知,所以两个子集的和都应该是sum/2(所以前提是sum不能是奇数),即题目转换成从这个数组里面选取一些元素使这些元素和为sum/2。如果我们将所有元素的值看做是物品的重量,每件物品价值都为1,所以这就是一个恰好装满的01背包问题。
- Coin Change(零钱兑换)
题目给定一个价值amount和一些面值,假设每个面值的硬币数都是无限的,问我们最少能用几个硬币组成给定的价值。
如果我们将面值看作是物品,面值金额看成是物品的重量,每件物品的价值均为1,这样此题就是是一个恰好装满的完全背包问题了。不过这里不是求最多装入多少物品而是求最少,我们只需要将完全背包的转态转移方程中的max改成min即可,又由于是恰好装满,所以除了dp[0],其他都应初始化为INT_MAX。
- Target Sum(目标和)
这道题给了我们一个数组(元素非负),和一个目标值,要求给数组中每个数字前添加正号或负号所组成的表达式结果与目标值S相等,求有多少种情况。
假设所有元素和为sum,所有添加正号的元素的和为A,所有添加负号的元素和为B,则有sum = A + B 且 S = A - B,解方程得A = (sum + S)/2。即题目转换成:从数组中选取一些元素使和恰好为(sum + S) / 2。可见这是一个恰好装满的01背包问题,要求所有方案数,将1.2节状态转移方程中的max改成求和即可。需要注意的是,虽然这里是恰好装满,但是dp初始值不应该是inf,因为这里求的不是总价值而是方案数,应该全部初始为0(除了dp[0]初始化为1)。
一些其他的dp问题
最长公共子串
$dp[i][j]$表示比较到$A[i],B[j]$时候的最长公共子串,且此时$A[i],B[j]$为最长公共子串的最后一个元素,故要求$A[i]=B[j]$
当$A[i]=B[j],dp[i][j]=dp[i-1][j-1]+1$,当$A[i]!=B[j],dp[i][j]=0$
答案是每次更新以后,记一个最大值就是答案
最长公共子序列
$dp[i][j]$表示比较到$A[i],B[j]$时候的最长公共子序列
当$A[i]=B[j],dp[i][j]=dp[i-1][j-1]+1$,$A[i]!=B[j],dp[i][j]=max(dp[i-1][j],dp[i][j-1])$
最长回文子序列
$dp[i][j]$表示字串从i到j的最长回文子序列长度
当$s[i]=s[j],dp[i][j]=dp[i+1][j-1]+2$,当$s[i]!=s[j],dp[i][j]=max(dp[i+1][j],dp[i][j-1])$注意i从n到1枚举,j从i+1到n枚举
最长回文子串
$dp[i][j]$表示$S_i,…,S_j$是否回文子串,1为是,0为否
当$s[i]=s[j],dp[i][j]=dp[i+1][j-1]+2$,当$s[i]!=s[j],dp[i][j]=0$
但枚举方式有区别,不能直接像回文序列一样枚举,因为不能保证$dp[i+1][j-1]$已经被计算过,故我们采取按回文子串长度来枚举,用一个数记录L最长长度
先初始化$dp[i][i]=1,dp[i][i+1]=1 (s[i]=s[i+1])$
之后从L从3到n,i从1到i+L-1<n枚举就行
N,NP,NPC,NP-hard
基础定义
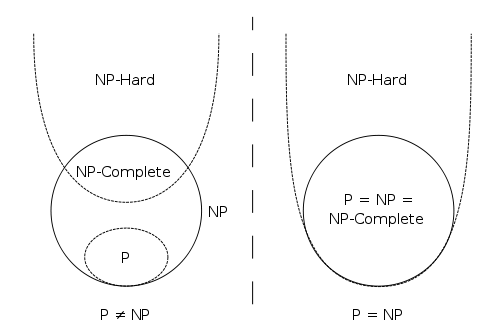
- P Problem:这个应该最易理解,就是一个问题能够在Polynominal的时间的获得解决,固然,是对于任意input size。
- NP Problem:对于一类问题,咱们可能没有一个已知的快速的方法获得问题的答案,可是若是给咱们一个candidate answer,咱们可以在polynominal的时间内验证这个candidate answer究竟是不是咱们已知问题的答案,这类问题叫作NP problem。因此很显然 P Problem是NP problem的一个子集。
- NP-hard Problem:对于这一类问题,用一句话归纳他们的特征就是“at least as hard as the hardest problems in NP Problem”, 就是NP-hard问题至少和NP问题同样难。
- NP-Complete Problem:对于这一类问题,他们知足两个性质,一个就是在polynomial时间内能够验证一个candidate answer是否是真正的解,另外一个性质就是咱们能够把任何一个NP问题在polynomial的时间内把他的input转化,使之成为一个NP-complete问题(即规约)。NP-Complete Problem问题能够互相转换 (在多项式时间内),只要其中一个问题能够在多项式时间内解决,那么其余问题也都将能够在多项式时间内解决。
规约——一种技巧
- 把P的输入转化到Q的输入;
- 把Q的输出转化到P的输出。
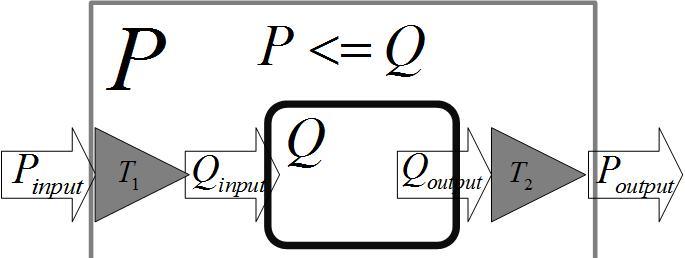
- 下图展现了上述规约过程。其中 $T_1 $在多项式时间将 P的输入 $P_{input }$转化成Q的输入 $Q_{input}$ ; T2 在多项式时间将 Q的输出$ Q_{output} $转化成P的输出$ P_{output} $。也就是说NP-hard问题 P 能够依赖于对问题 Q 的解决而解决。那么 Q 至少比 P 要难,即 P<=Q 。
如何对问题证实
下面来列出了一些常见的证实问题及其证实套路。
证实NP问题:这个容易,即给你一个结果,你能在polynomial的时间内验证该结果的正确性。
证实NP-hard问题:咱们要证实一个问题是NP-hard的时候,咱们一般要作的是找到一个已被证实了的NPC问题,并把这个NPC问题归约到该问题上去(即NPC<=NP-hard)。
证实NP-Complete问题
分如下两步:
- 第一步证实这个问题属于NP;
- 第二步,证实这个问题是NP-hard的。也就是找一个NPC问题把它规约过去
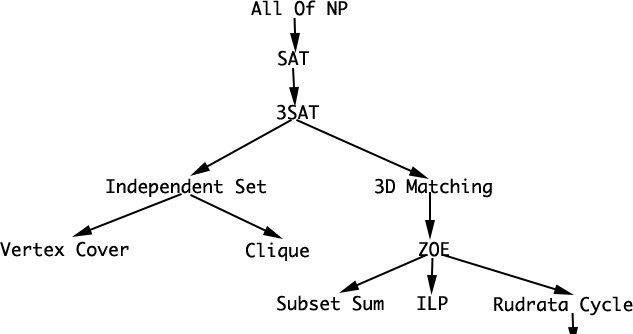
下图列出了几个已被发现NP-Complete问题,及其规约关系。能够看出全部的NP问题均可以规约到SAT(即NP<=SAT),也就是说SAT至少与NP问题同样难,或者若是解决了3SAT问题,全部的NP问题就解决了。一样的,SAT<=3SAT,3SAT<=Independent Set,Independent Set<=Vertex Cover OR Clique。算法
规约关系具备传递性,因此有3SAT<=Vertex Cover,NP<=NP-Complete。 事实上,因为NP-Complete ⊂ NP 且 NP<=NP-Complete,能够推导出 全部的NP-Complete 能够相互规约,也就是全部的NP-Complete都是等价的。