清完稿子终于有时间来干正事了 时隔快一个月俺终于开坑了
主要目的是复习一下C&C++相关的知识
为下学期的cs100准备一下
顺便带上基础算法复习 排序算法(10种),二分,堆栈模拟,贪心等
题目以模拟为主
首先是C&C++部分的 比较预习x
以及因为懒栗子我基本照搬菜鸟教程(
会的东西不会提及大概是注重以前没注意过的
最近好像C#很流行?也许会顺带看一下
C&C++
首先个人认为表面上看这俩最大区别是STL库
c++因为有了很多快捷的算法和函数之类的东西
还是先复习变量
ps:如果是c和c++共通的东西,会用c来举例子
如果不同会分两种写的
基本变量
| 类型 | 描述 |
|---|---|
| char | 通常是一个字节(八位), 这是一个整数类型。 |
| int | 整型,4 个字节,取值范围 -2147483648 到 2147483647。 |
| float | 单精度浮点值。单精度是这样的格式,1位符号,8位指数,23位小数。 |
| double | 双精度浮点值。双精度是1位符号,11位指数,52位小数。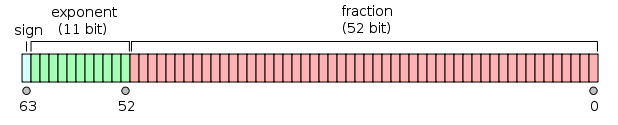 |
| void | 表示类型的缺失。 |
| long long | - 9223372036854775808 ~ 9223372036854775807(20位十进制数) |
关于C&C++的关键字
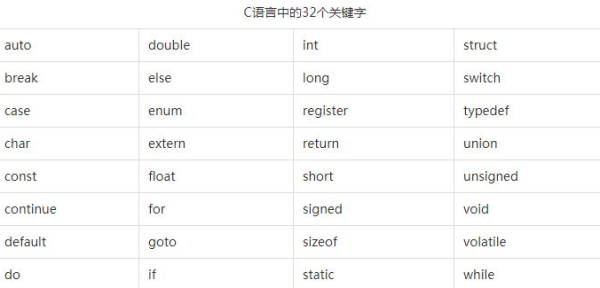
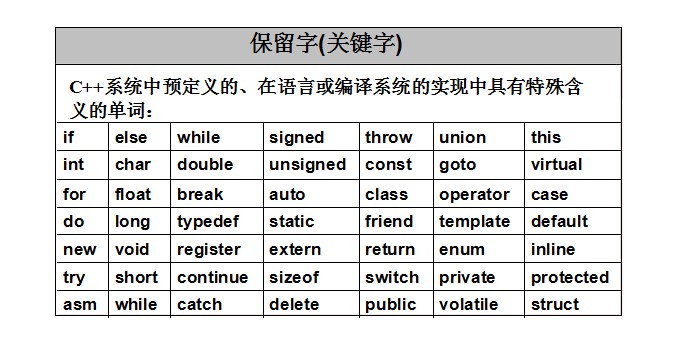
输出格式
1.转换说明符
%a(%A) 浮点数、十六进制数字和p-(P-)记数法(C99)
%c 字符
%d 有符号十进制整数
%f 浮点数(包括float和double)
%e(%E) 浮点数指数输出[e-(E-)记数法]
%g(%G) 浮点数不显无意义的零”0”
%i 有符号十进制整数(与%d相同)
%u 无符号十进制整数
%o 八进制整数 e.g. 0123
%x(%X) 十六进制整数
%p 指针
%s 字符串
%% “%”
2.标志
左对齐:”-“ e.g. “%-20s”
右对齐:”+” e.g. “%+20s”
空格:若符号为正,则显示空格,负则显示”-“ e.g. “% “
#:对c,s,d,u类无影响;对o类,在输出时加前缀o;对x类,在输出时加前缀0x;
对e,g,f 类当结果有小数时才给出小数点。
3.格式字符串(格式)
[标志][输出最少宽度][.精度][长度]类型
“%-md” :左对齐,若m比实际少时,按实际输出。
“%m.ns”:输出m位,取字符串(左起)n位,左补空格,当n>m or m省略时m=n
e.g. “%7.2s” 输入CHINA
输出” CH”
“%m.nf”:输出浮点数,m为宽度,n为小数点右边数位
e.g. “%” 输入3852.99
输出3853.0
长度:为h短整形量,l为长整形量
printf的格式控制的完整格式:
% - .n l或h 格式字符
下面对组成格式说明的各项加以说明:
①%:表示格式说明的起始符号,不可缺少。
②-:有-表示左对齐输出,如省略表示右对齐输出。
③0:有0表示指定空位填0,如省略表示指定空位不填。
④m.n:m指域宽,即对应的输出项在输出设备上所占的字符数。N指精度。用于说明输出的实型数的小数位数。为指定n时,隐含的精度为n=6位。
⑤l或h:l对整型指long型,对实型指double型。h用于将整型的格式字符修正为short型。
关于extern
extern用于声明某一个变量而并非定义
个人感觉和py的global很像,很tm适合出题??
但好像只有这一个extern是用来声明全局变量?基本就是一个global的感觉
#include <stdio.h>
#include <iostream>
#include <cstdio>
// 函数外定义变量 x 和 y
using namespace std;
int x;
int y;
int addtwonum()
{
// 函数内声明变量 x 和 y 为外部变量
extern int x;
extern int y;
// 给外部变量(全局变量)x 和 y 赋值
x = 1;
y = 2;
return x+y;
}
int main()
{
int result;
// 调用函数 addtwonum
result = addtwonum();
printf("result 为: %d\n",result);
cout<<x<<' '<<y;
// 3
// 1 2
return 0;
依旧感觉没什么卵用md
但感谢菜鸟教程告诉我了一个用途,在引用自己写的类似包?的时候的用的
如果需要在一个源文件中引用另外一个源文件中定义的变量,我们只需在引用的文件中将变量加上 extern 关键字的声明即可。
addtwonum.c 文件代码:
#include <stdio.h> /*外部变量声明*/
extern int x ;
extern int y ;
int addtwonum()
{
return x+y;
}
test.c 文件代码:
#include <stdio.h> /*定义两个全局变量*/
int x=1;
int y=2;
int addtwonum();
int main()
{
int result;
result = addtwonum();
printf("result 为: %d\n",result);
return 0;
}
当上面的代码被编译和执行时,它会产生下列结果:
$ gcc addtwonum.c test.c -o main
$ ./main
result 为: 3
文件的读入与写入
c++的话很方便
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
很简单在main的开头加两句就行
c的话有点麻烦
写入文件
首先是有几个模式
| 模式 | 描述 |
|---|---|
| r | 打开一个已有的文本文件,允许读取文件。 |
| w | 打开一个文本文件,允许写入文件。如果文件不存在,则会创建一个新文件。在这里,您的程序会从文件的开头写入内容。如果文件存在,则该会被截断为零长度,重新写入。 |
| a | 打开一个文本文件,以追加模式写入文件。如果文件不存在,则会创建一个新文件。在这里,您的程序会在已有的文件内容中追加内容。 |
| r+ | 打开一个文本文件,允许读写文件。 |
| w+ | 打开一个文本文件,允许读写文件。如果文件已存在,则文件会被截断为零长度,如果文件不存在,则会创建一个新文件。 |
| a+ | 打开一个文本文件,允许读写文件。如果文件不存在,则会创建一个新文件。读取会从文件的开头开始,写入则只能是追加模式。 |
#include <stdio.h>
int main()
{
FILE *fp = NULL;// 先是创建一个文件指针?
fp = fopen("/tmp/test.txt", "w+");
fprintf(fp, "This is testing for fprintf...\n");
fputs("This is testing for fputs...\n", fp);//两种用法
fclose(fp);
}
读入文件
#include <stdio.h>
int main()
{
FILE *fp = NULL;
char buff[255];
fp = fopen("/tmp/test.txt", "r");
fscanf(fp, "%s", buff);//这个遇到第一个空格和换行符时,它会停止读取。
printf("1: %s\n", buff );//This
fgets(buff, 255, (FILE*)fp);//函数 fgets() 从 fp 所指向的输入流中读取 n - 1 个字符。它会把读取的字符串复制到缓冲区 buf,并在最后追加一个 null 字符来终止字符串。如果这个函数在读取最后一个字符之前就遇到一个换行符 '\n' 或文件的末尾 EOF,则只会返回读取到的字符,包括换行符。
printf("2: %s\n", buff );//is testing for fprintf...
fgets(buff, 255, (FILE*)fp);
printf("3: %s\n", buff );//This is testing for fputs...
fclose(fp);
}
关于和字符,字符串有关的读入复习
scanf("%s",&s);//常用的字符读入,读到空格为止,空格不会被跳过
gets(s);//读到换行符为止,不读换行符会跳过
scanf("%s",&s);getchar();scanf("%c%d",&ch,&x);//这几个一起读入的时候,适当getchar()来处理空格问题
scanf("%7s",&s);//只读前7位,后面输入的不管
while(scanf("%s",&s)!=EOF)//一直读入,知道遇到EOF为止,在windows里面是CTRL+Z
三元运算符
就是常用的if语句,简短精炼,但可读性极差
复习一下规则
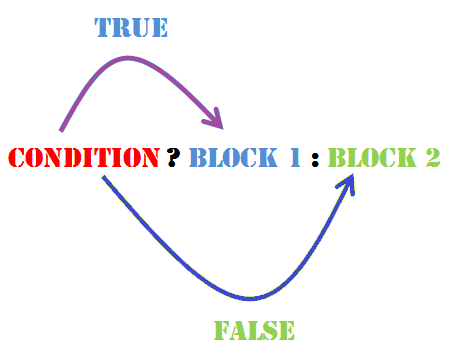
枚举
C中一个很神奇的定义,虽然我觉得用处不大,但是没有见过还是写一下
enum DAY //名称可以省略
{
MON=1, TUE, WED, THU, FRI=10, SAT, SUN//默认后一个值为前一个+1,徐洪剑可以跳跃赋值
} day;
// 1 2 3 4 10 11 12
实际调用如下
#include <stdio.h>
enum DAY
{
MON=1, TUE, WED, THU, FRI, SAT, SUN
};
int main()
{
enum DAY day;
day = WED;
printf("%d",day);
for (day = MON; day <= SUN; day++)
{
printf("枚举元素:%d \n", day);
}//只有连续的枚举可以遍历
return 0;
}
指针
定义
每一个储存的变量,都有一个与其对应的储存地址,指针便是指向这个地址,调用该地址的用途
简单的例子
#include <stdio.h>
int main ()
{
int var = 20; /* 实际变量的声明 */
int *ip; /* 指针变量的声明 */
ip = &var; /* 在指针变量中存储 var 的地址 */
printf("var 变量的地址: %p\n", &var );
/* 在指针变量中存储的地址 */
printf("ip 变量存储的地址: %p\n", ip );
/* 使用指针访问值 */
printf("*ip 变量的值: %d\n", *ip );
return 0;
//var 变量的地址: 0x7ffeeef168d8
//ip 变量存储的地址: 0x7ffeeef168d8
//*ip 变量的值: 20
//sizeof(&var) 查询指针的大小
}
NULL指针
在变量声明的时候,如果没有确切的地址可以赋值,为指针变量赋一个 NULL 值是一个良好的编程习惯。赋为 NULL 值的指针被称为空指针。
NULL 指针是一个定义在标准库中的值为零的常量。
举个栗子
#include <stdio.h>
int main ()
{
int *ptr = NULL;
printf("ptr 的地址是 %p\n", ptr );
//ptr 的地址是 0x0
return 0;
}
指针的算术运算
指针支持++,–,+,- 总的来说就是可以对地址进行加减来实现遍历作用
举个栗子
#include <stdio.h>
const int MAX = 3;
int main ()
{
int var[] = {10, 100, 200};
int i, *ptr;
/* 指针中的数组地址 */
ptr = var;//最开始默认为一个数字的位置
//ptr = &var[MAX-1];最后一个位置
for ( i = 0; i < MAX; i++)
{
printf("存储地址:var[%d] = %p\n", i, ptr );
printf("存储值:var[%d] = %d\n", i, *ptr );
/* 指向下一个位置 */
ptr++;
}
return 0;
}
指针可以用关系运算符进行比较,如 ==、< 和 >
这个很好理解 不解释了
指针数组
数组的地址就是储存第一位的地址
指针指向的内容可以是数字或者字符
都可以自己定义
试了一下好像如果是数字不能随便乱搞?
int指向int是不行的,反正有问题 ,要用只能用系统的地址不能瞎搞
#include <stdio.h>
const int MAX = 3;
int main ()
{
int var[] = {10, 100, 200};
int i, *ptr[MAX];
for ( i = 0; i < MAX; i++)
{
ptr[i] = &var[i]; /* 赋值为整数的地址 */
}
for ( i = 0; i < MAX; i++)
{
printf("Value of var[%d] = %d\n", i, *ptr[i] );
}
return 0;
}
字符
#include <stdio.h>
const int MAX = 4;
int main ()
{
const char *names[] = {
"Zara Ali",
"Hina Ali",
"Nuha Ali",
"Sara Ali",
};//定义指针指向字符串
int i = 0;
for ( i = 0; i < MAX; i++)
{
printf("Value of names[%d] = %s\n", i, names[i] );
printf("loc of names[%d] = %d\n", i, *names[i] );//储存地址打印
}
/*Value of names[0] = Zara Ali
loc of names[0] = 90
Value of names[1] = Hina Ali
loc of names[1] = 72
Value of names[2] = Nuha Ali
loc of names[2] = 78
Value of names[3] = Sara Ali
loc of names[3] = 83*/
return 0;
}
很有趣的是用指针定义的字符串和直接用数组定义的字符串,他们两个的地址差距很大x
多重指针
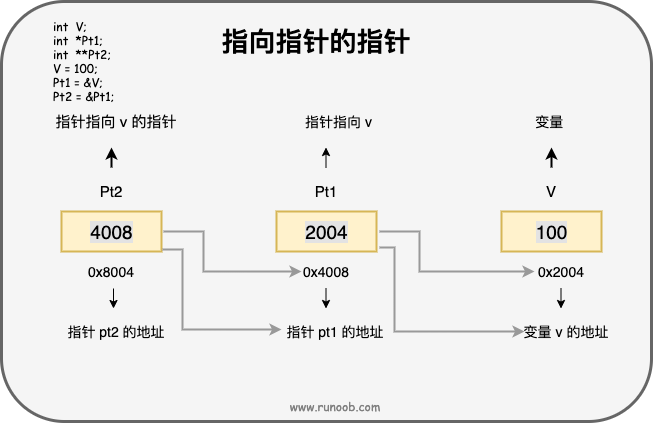
总之还是很好理解的,能套很多层
函数与指针
函数里也允许定义和传递指针,这个也很好理解
也允许函数的返回值是指针
但有一个要注意的地方
C&C++不支持在调用函数时返回局部变量的地址,除非定义局部变量为 static 变量。
栗子
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
/* 要生成和返回随机数的函数 */
int * getRandom( )
{
static int r[10];//必须这样写
int i;
/* 设置种子 */
srand( (unsigned)time( NULL ) );
for ( i = 0; i < 10; ++i)
{
r[i] = rand();
printf("%d\n", r[i] );
}
return r;
}
/* 要调用上面定义函数的主函数 */
int main ()
{
/* 一个指向整数的指针 */
int *p;
int i;
p = getRandom();
for ( i = 0; i < 10; i++ )
printf("*(p + [%d]) : %d\n", i, *(p + i) );
return 0;
}
C 不支持在调用函数时返回局部变量的地址,除非定义局部变量为 static 变量。
因为局部变量是存储在内存的栈区内,当函数调用结束后,局部变量所占的内存地址便被释放了,因此当其函数执行完毕后,函数内的变量便不再拥有那个内存地址,所以不能返回其指针。
除非将其变量定义为 static 变量,static 变量的值存放在内存中的静态数据区,不会随着函数执行的结束而被清除,故能返回其地址。
感觉理解的不算很透彻,后期再继续补充
手写swap
用了指针的写法,反正很绕
void swap(int *a,int *b)
{
int tmp;
tmp=*a;
*a=*b;
*b=tmp;
}
swap(&a,&b);
链表
一个无语的东西
在写c代码的时候,无意中发现nmd为什么c不支持定义的时候直接赋值???实属弱智操作,每次写循环tmd都要把i放在外面写,乌鱼子 (原来是我没有c11,小丑竟是我自己(
补充,c没有class气死我了
动态内存
malloc()函数,用于向系统申请内存
free()释放malloc或calloc、realloc函数给指针变量分配的内存空间的函数使用后该指针变量一定要重新指向NULL,防止野指针出现,有效 规避误操作。
int main()
{
int size=10;
float *pArray=NULL;
pArray=(float *)malloc(sizeof(float)*size);//将size大小的float空间赋给指针
memset(pArray,0,sizeof(float)*size);
/*access the array*/
free(pArray);
return 0;
}
算法复习
用于练习,不做特殊说明都用c来编写
十大排序算法
首先写一下基本的相关定义
1、稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为稳定排序。
2、非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。
3、原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
4、非原地排序:需要利用额外的数组来辅助排序。
ps:由于原po很作死想写伪sort代替,于是引入了begin和end参数,导致某些过程变得十分复杂,大家千万不要学我
一下代码全部是原po自己手撸的,一定不是最简写法,也不好看,就是很好理解,简单来说就是:下面请欣赏Aoki_Umi用作死的c手撸十大排序算法~
介绍也比较通俗XD
为什么缩进这么奇怪:\别问,问就是vs自带的
冒泡排序
算法介绍
冒泡排序作为一种比较经典的算法也算是很好理解的,每次遍历找出最大的数把它依次排在末尾,找到最大的数的方式就是比较相邻两个数的大小,越大的数越往后面移动,全遍历找一遍就行了
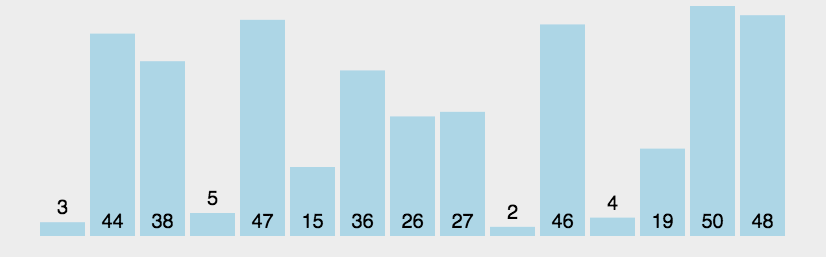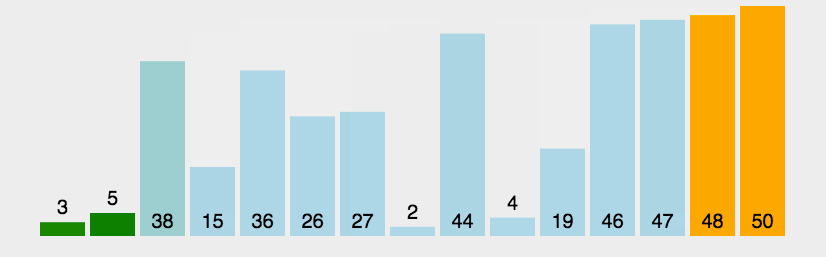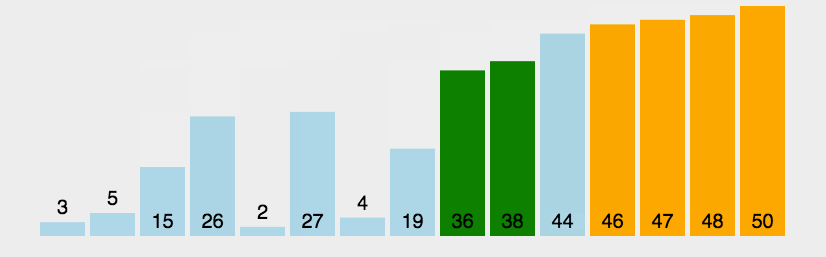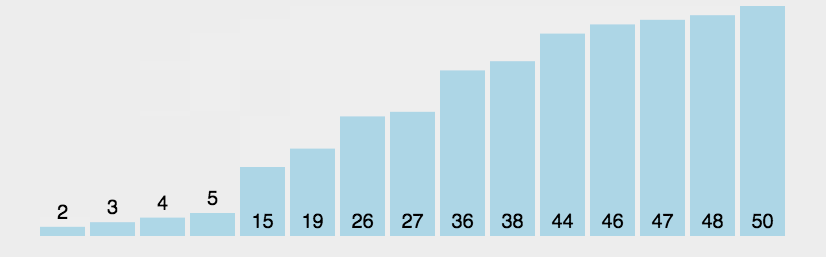
复杂度
时间$O(n^2)$ 最优$O(n)$空间$O(1)$ 总的来说还是很慢的
稳定性
稳定排序 ,原地排序
代码实现
普通版本:
void sort_Bubble (int num[100],int begin,int end)
{
int i;
for (i = end; i > begin; i--)
{
int j;
for (j = begin; j < i;j++)
{
if(num[j]>num[j+1])
{
int tmp;
tmp= num[j+1];
num[j+1] = num[j];
num[j] = tmp;
}
}
}
}
优化版本:
假如从开始的第一对到结尾的最后一对,相邻的元素之间都没有发生交换的操作,这意味着右边的元素总是大于等于左边的元素,此时的数组已经是有序的了,我们无需再对剩余的元素重复比较下去了。
void sort_Bubble (int num[100],int begin,int end)
{
int i;
for (i = end; i > begin; i--)
{
int j, flag = 0;
for (j = begin; j < i;j++)
{
if(num[j]>num[j+1])
{
int tmp;
tmp= num[j+1];
num[j+1] = num[j];
num[j] = tmp;
flag = 1;
}
}
if(flag==0)
break;
}
}
选择排序
算法介绍
冒泡排序是选最大往后堆,那么选择排序就是每次找最小的往前堆。找的方法为,把序列分为有序列$R1[1,2,…,i]$与无序列(没有排序过的原始序列)$R2[i+1,i+2,…,n]$两大段,每次找出无序列中最小的元素与无序列中第一个元素交换位置,如此有序列长度逐渐增加直到整个序列有序。
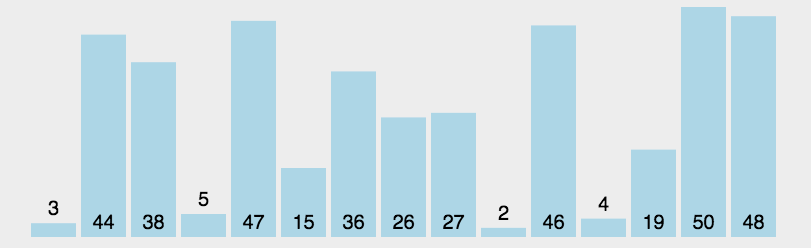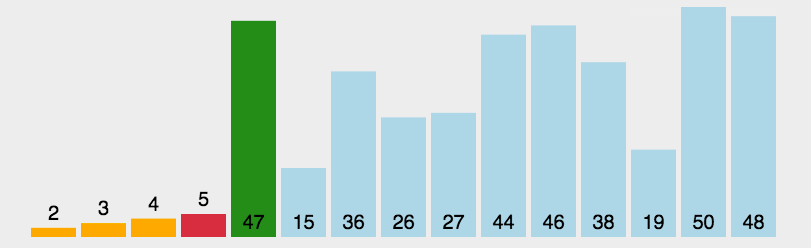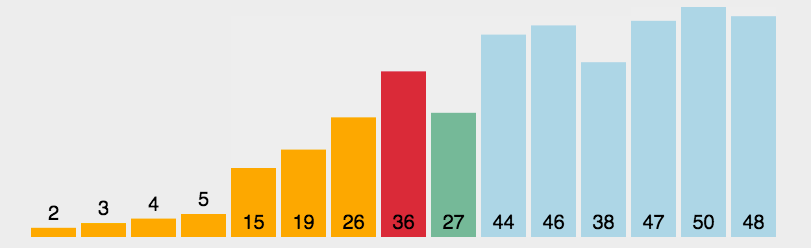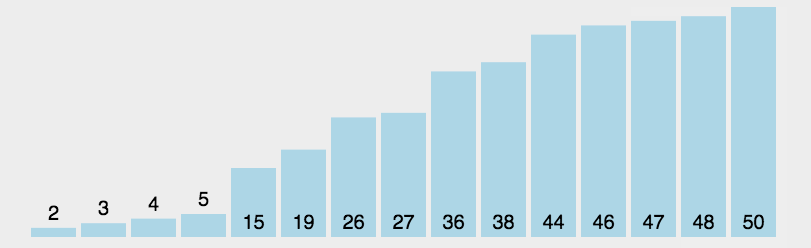
复杂度
时间$O(n^2)$无论如何都是$O(n^2)$,空间$O(1)$,实在是慢
稳定性
非稳定排序 ,原地排序
代码实现
void sort_selection(int num[100],int begin,int end)
{
int i;
for (i = begin; i <end;i++)
{
int j,min;
min = i;
for (j = i + 1; j <= end;j++)
{
if(num[j]<num[min])
{
min = j;
}
}
int tmp;
tmp = num[i];
num[i] = num[min];
num[min] = tmp;
}
}
插入排序
算法介绍
这个算法形象说就是每次把后面一个没排过序的元素不断往有序的元素里面插,从后往前扫,为啥觉得越来越低效了(bushi 这玩意需要手写队列。。。。说实话用c++堆好像是不是好很多(其实就是快乐的优先队列)越来越复杂了x
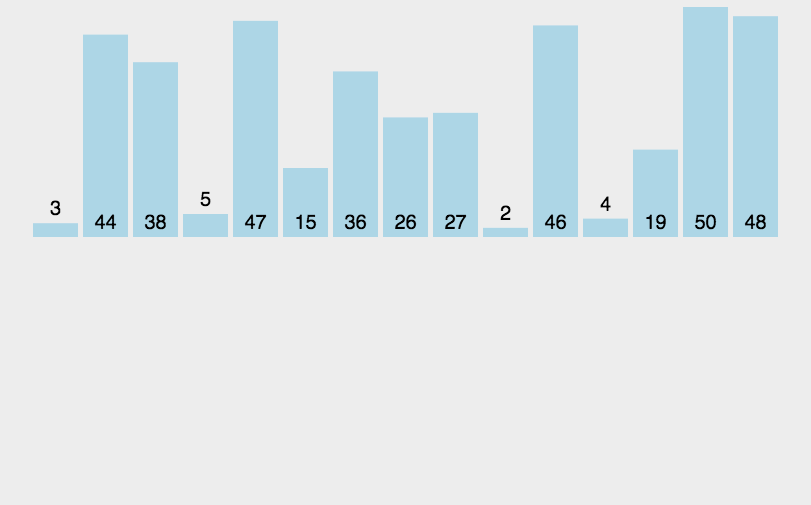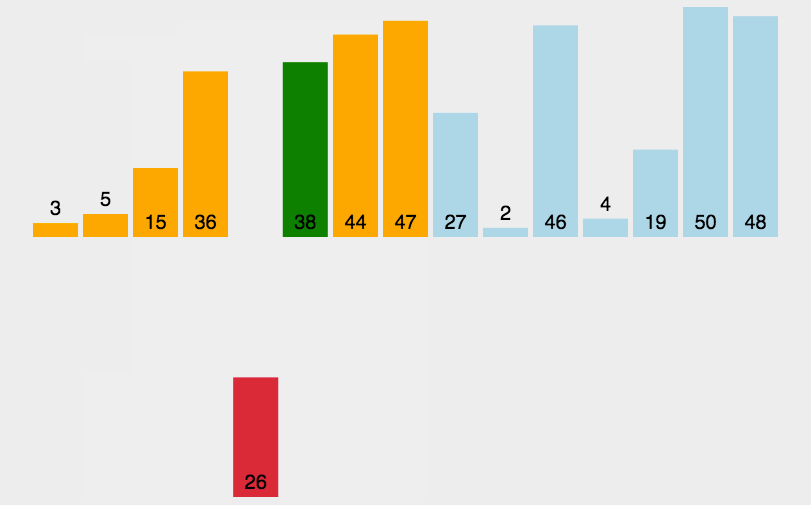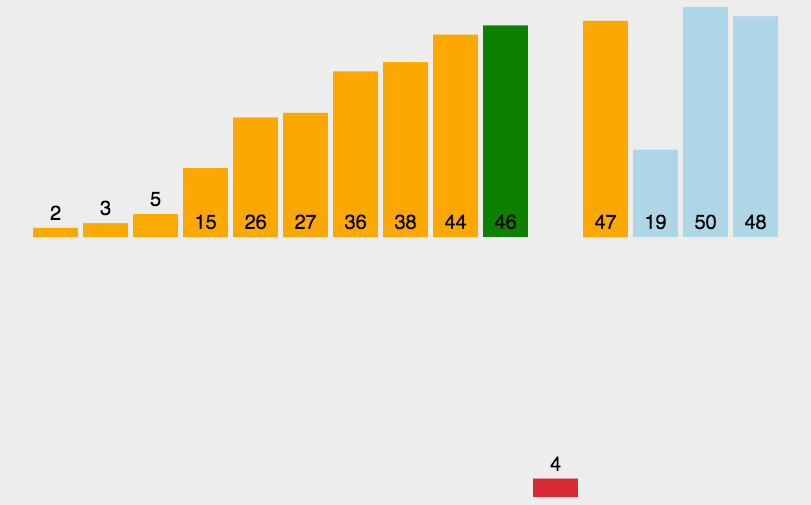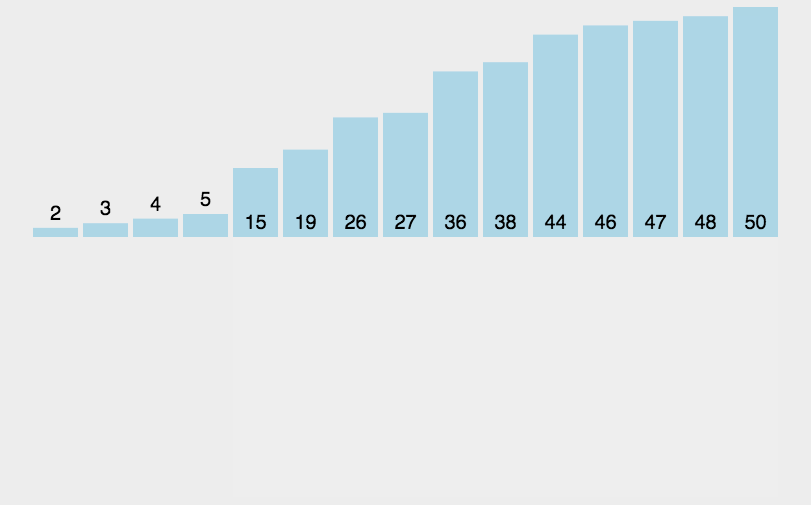
复杂度
时间$O(n^2)$无论如何都是$O(n^2)$,空间$O(1)$,实在是慢
稳定性
稳定排序 ,原地排序
代码实现
void sort_insertion(int num[],int begin,int end)
{
int i;
for (i = begin+1; i <= end;i++)
{
int tmp;
tmp = num[i];
int j;
if(num[begin]>num[i])//由于我多了参数为了防止意外我写了特判x
j = begin - 1;
else
{
for (j = i-1; j >=begin;j--)
if(num[j]<=tmp)
break;
}
//j+1是要插入的位置
int k;
for (k = i; k > j + 1;k--)
num[k] = num[k - 1];
num[j + 1] = tmp;
}
}
希尔排序
算法介绍
是插入排序的优化版本,每次把序列分成len/2组,每组跨元素相邻如图所示,每次按组来进行插入排序,以达到优化的效果
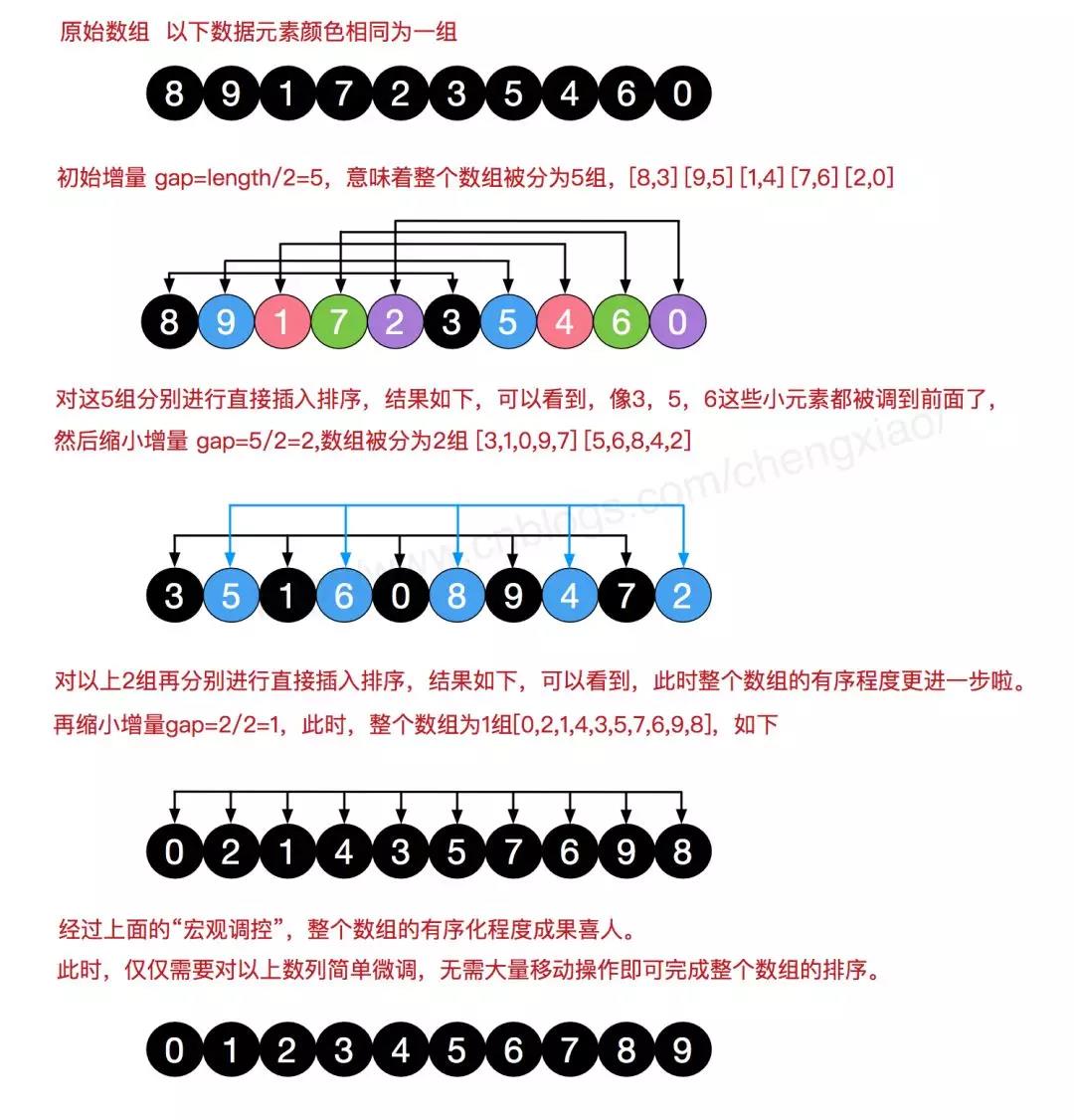
复杂度
时间$O(n^{1.3})$最优$O(n)$最坏$O(n^2)$空间$O(1)$ 玄学的东西
稳定性
非稳定排序 ,原地排序
代码实现
此代码我撸的异常艰辛,主要是因为,太绕了。。。,加了奇怪的参数后
void sort_shell(int num[],int begin,int end)
{
int gap;
void I_sort(int new_begin,int new_end,int g)
{
int i;
for (i = new_begin+g; i <= new_end;i++)
{
int tmp;
tmp = num[i];
int j;
if(num[new_begin]>num[i])
j = new_begin - g;
else
{
for (j = i-g; j >=new_begin;j-=g)
if(num[j]<=tmp)
break;
}
//j+1是要插入的位置
int k;
for (k = i; k > j + g;k-=g)
num[k] = num[k - g];
num[j + g] = tmp;
}
}
int len;
len = end - begin + 1;
for(gap= len / 2; gap > 0;gap/=2)
{
int i,j;
for (i = begin,j=end-gap+1; i < begin + gap;i++,j++)
I_sort(i, j, gap);
}
}
归并排序
算法介绍
一款很线段树的排序算法x分治思想易于理解。
主要思路是把区间每次一分为二,不断拆分成小的区间,每次大区间由两个已经有序的小区间合并,不断变得有序的过程。
问题是如何实现合并呢,这里用到的就是两个队列了。由于子区间一定有序,每次只要比较两个队列队头的大小,将小的加入新队列并将其弹出,直到一个队列元素全部弹完停止循环,就很好理解。
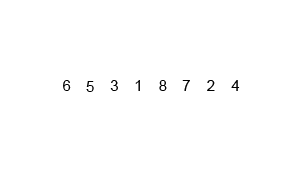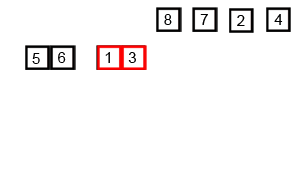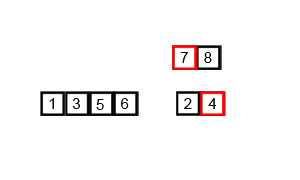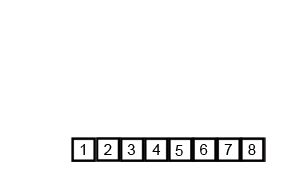
复杂度
时间$O(nlogn)$空间$O(n)$这很线段树
稳定性
稳定排序 ,非原地排序
代码实现
一举成功,一气呵成,爽
void sort_merge(int num[],int begin,int end)
{
void merge(int l,int mid,int r)
{
int fr1, fr2,tl1,tl2;
fr1 = l;
fr2 = mid + 1;
tl1 = mid;
tl2 = r;
int new[r - l + 1], i,flag;
flag = 0;
for (i = 1; i <= r - l + 1;i++)
{
if(fr1>tl1)
{
flag = 1;
break;
}
if(fr2>tl2)
break;
if(num[fr1]>num[fr2])
{
new[i] = num[fr2];
fr2++;
}
else
{
new[i] = num[fr1];
fr1++;
}
}
if(flag==0)
{
for (i; i <= r - l + 1;i++,fr1++)
new[i] = num[fr1];
}
else
{
for (i; i <= r - l + 1;i++,fr2++)
new[i] = num[fr2];
}
int j;
for (j = 1; j <= r - l + 1;j++)
num[l + j - 1] = new[j];
}
void split(int l,int r)
{
if(l==r)
return;
int mid;
mid = (l + r) / 2;
split(l, mid);
split(mid + 1, r);
merge(l, mid, r);
}
split(begin, end);
}
快速排序
算法介绍
其实写这篇的主要原因就是你校夏令营面试的题目。。。。当初他让我介绍快速排序,然而我对快排一无所知。。于是就一直很想写一个排序算法介绍orz
快排是一个运用很广泛的排序算法吧,主要思想也是分治,但叙述起来比较麻烦。
主要分为三步:①找一个基准(普通来说直接选区间第一个)②通过位置的比较交换让该基准左边数都小于他,右边数都大于他,于是该数的位置就确定了③再把两边的区间重复这个操作直到每个数都找到自己的位置x
比较抽象的就是如何让他左边都大于自己,右边都小于自己(说实话下面这个图我看不懂)
我看到的另一种解释比较容易理解:将序列看作也该双端队列两个指针fr,tl分别指向队头和队尾,以及一个当前变量x。
首先令x=a[fr]也就是先把第一个当作基准
再从队尾往前扫找到比x小的第一个数,a[fr]=a[tl]将其放在之前x的位置
再从队头开始往后扫找到比x大的第一个数,a[tl]=a[fr]将其放在之前队尾指向的位置
如此不断循环直到fr==tl,a[fr]=a[tl]=x如此这般,x就找到位置了。
通俗来讲就是用小的数填充靠前的位置,大的数填充靠后的位置,最后剩下的就是x的位置了
这个就很好理解,手撸应该挺容易x
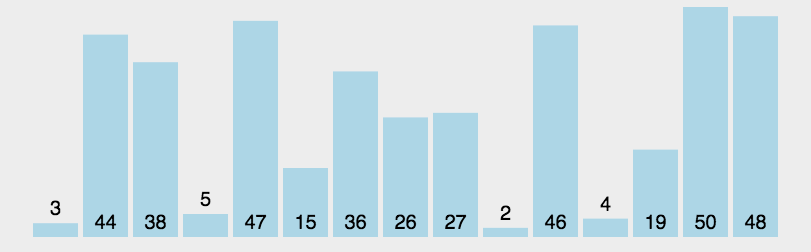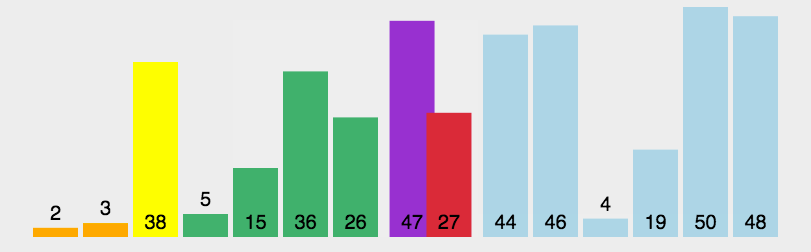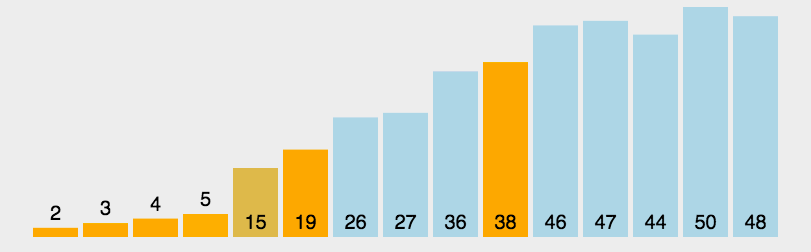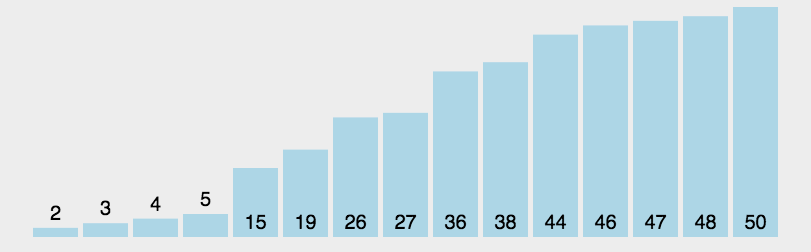
复杂度
时间$O(nlogn)$最坏$O(n^2)$空间$O(nlogn)$
稳定性
非稳定排序,原地排序
代码实现
有些头尾端点情况判断也要注意,稍微调一下就行
void sort_quick(int num[],int begin,int end)
{
int find_place(int l,int r)
{
int x, fr, tl;
x = num[l];
fr = l;
tl = r;
while(tl>fr)
{
while(fr<tl&&num[tl]>=x)
tl--;
if(tl==fr)
break;
num[fr] = num[tl];
fr++;
while(fr<tl&&num[fr]<=x)
fr++;
if(tl==fr)
break;
num[tl] = num[fr];
tl--;
}
num[fr] = x;
return fr;
}
void split(int l,int r)
{
if(l>=r)
return;
int loc;
loc = find_place(l, r);
split(l, loc-1);
split(loc + 1, r);
}
split(begin, end);
}
堆排序
算法介绍
这个要运用二叉树,大根堆小根堆的知识了,属于比较高级的算法。
二叉树就不解释了,主要谈谈大根堆和小根堆 优质博客
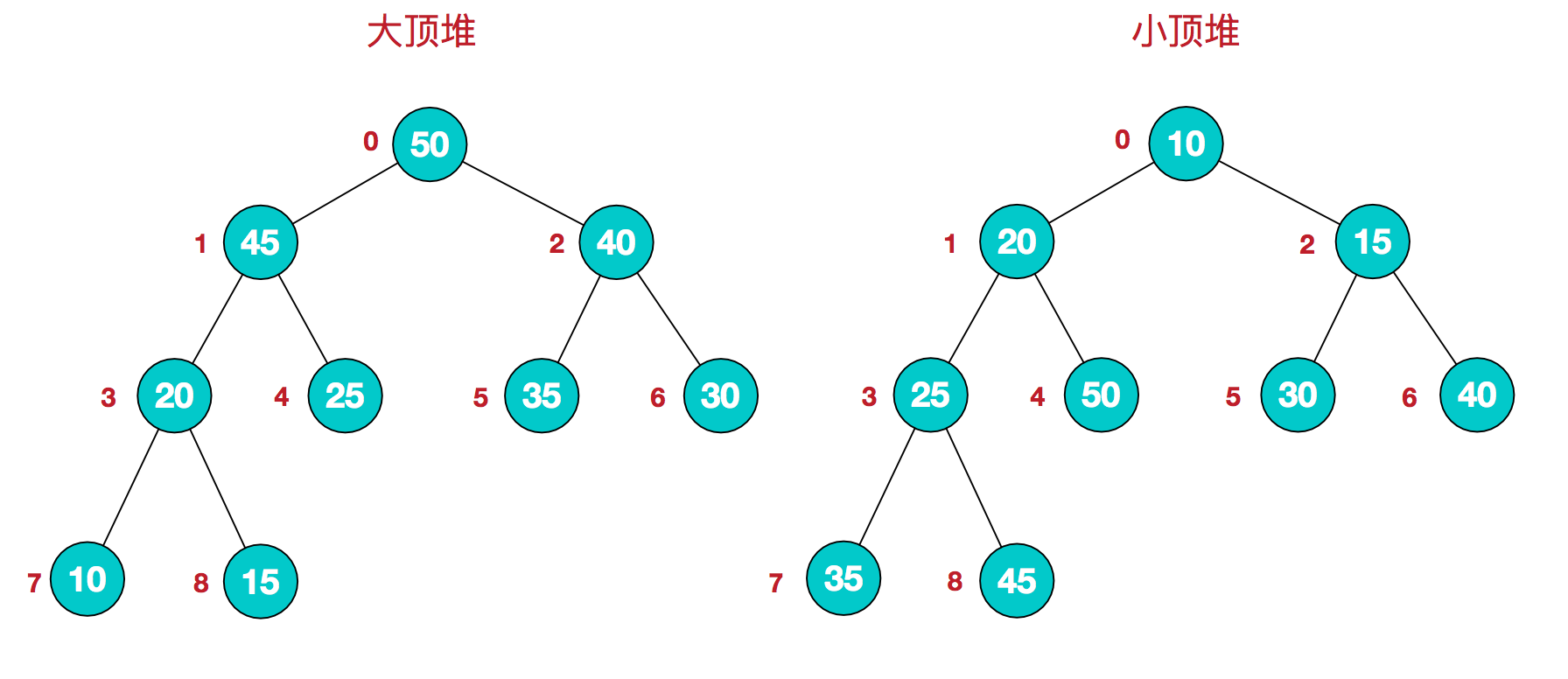

大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
图非常好懂了就不解释了
而堆排序就是以此为基础的排序算法.
方法是:①首先以原始序列为基础构建大/小根堆,示例为大根堆.②每次将堆顶与为末尾的无序元素交换,并交换后重新调整堆的结构使其仍然是大根堆③不断重复此交换直到序列全部有序
但怎么建立一个大根堆呢?
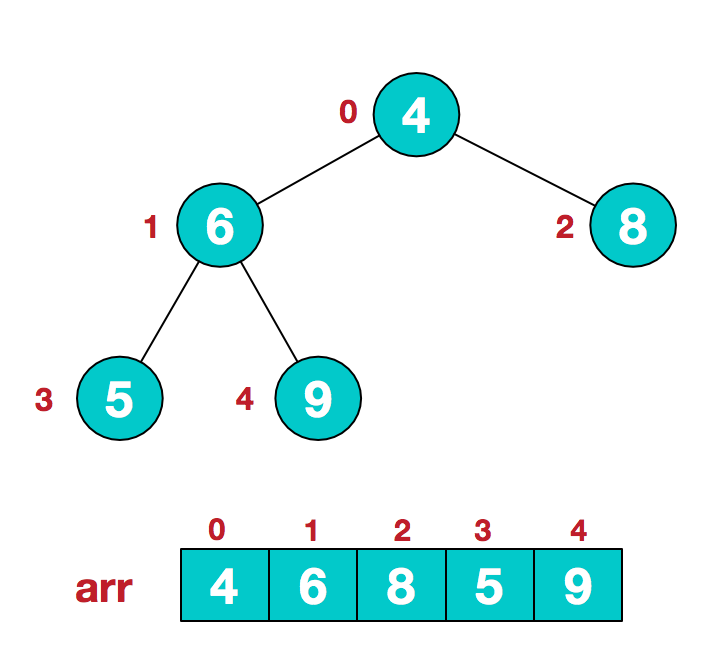
我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。像图例不断交换
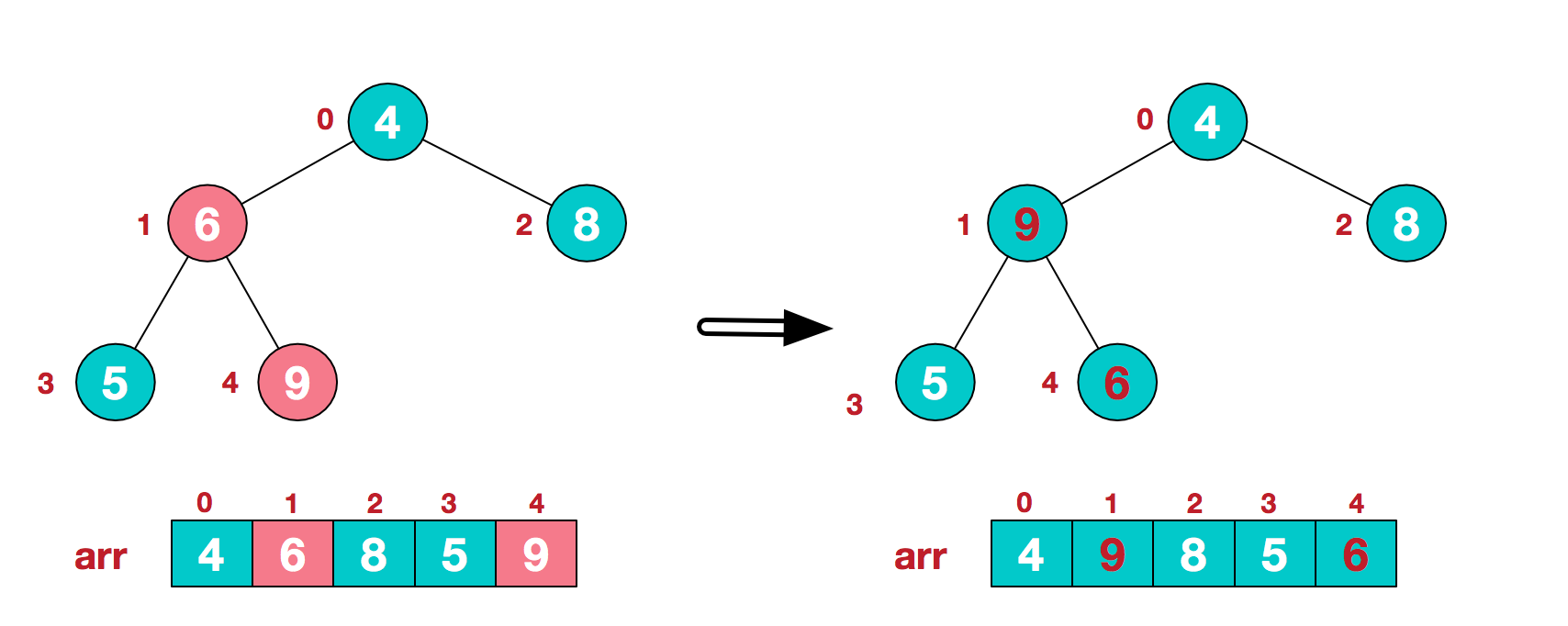
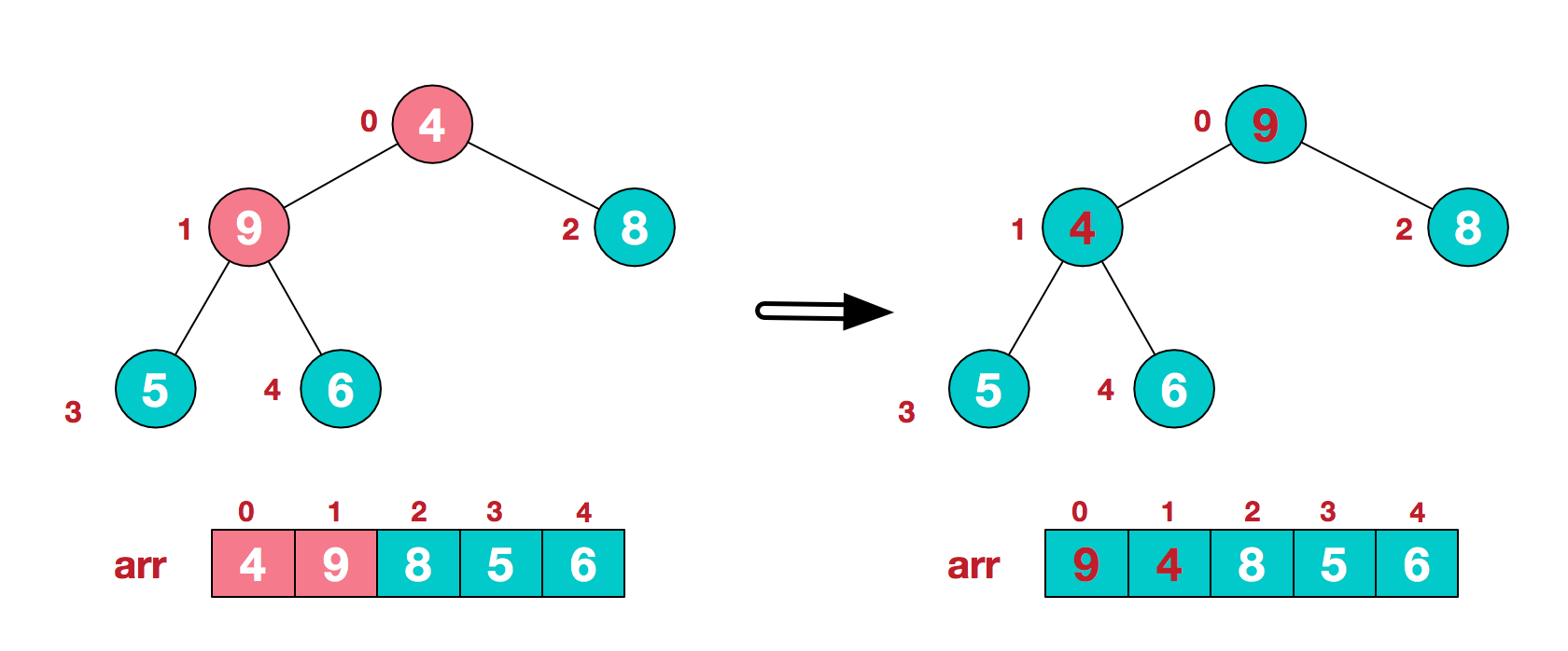
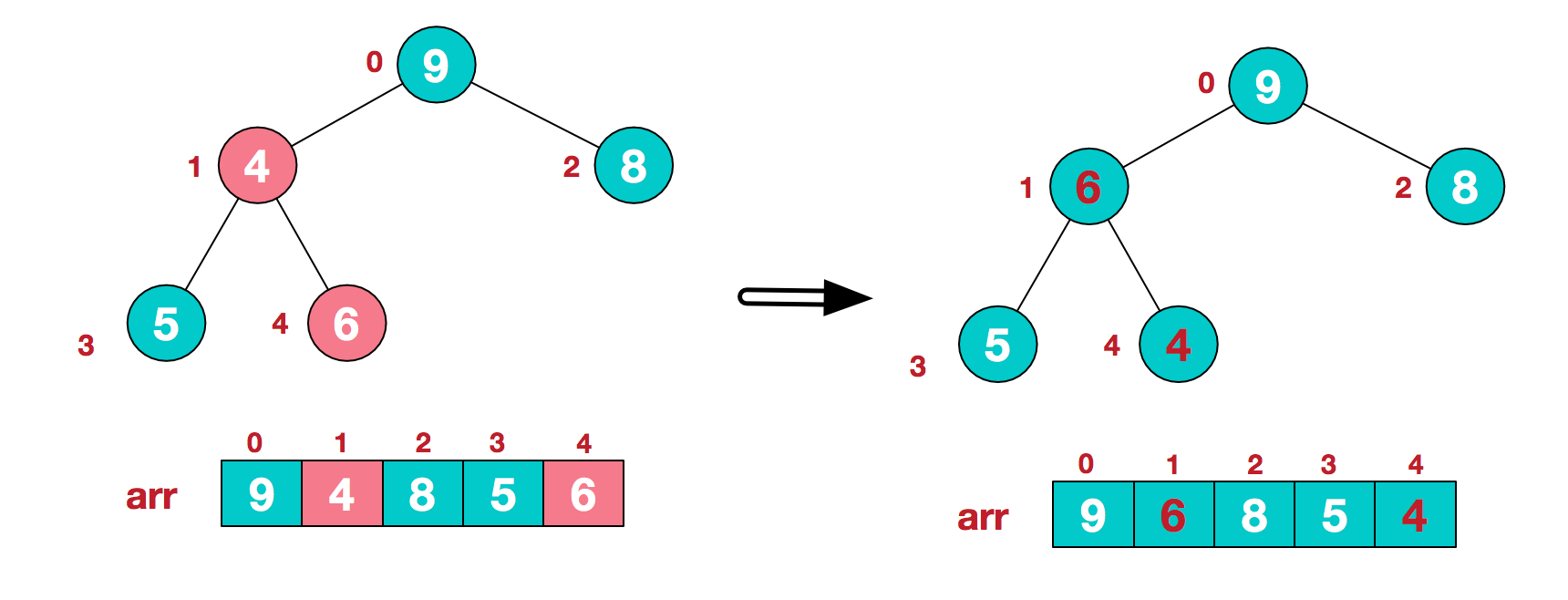
下面是形象表示交换的过程w
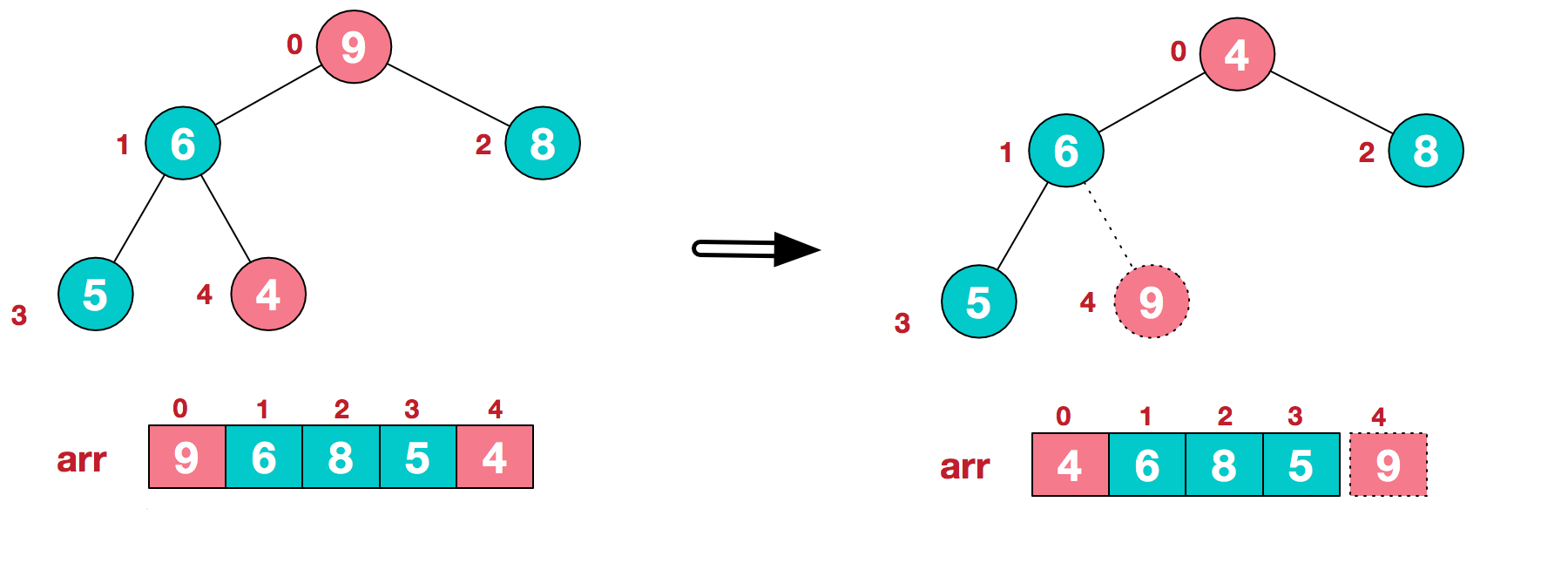
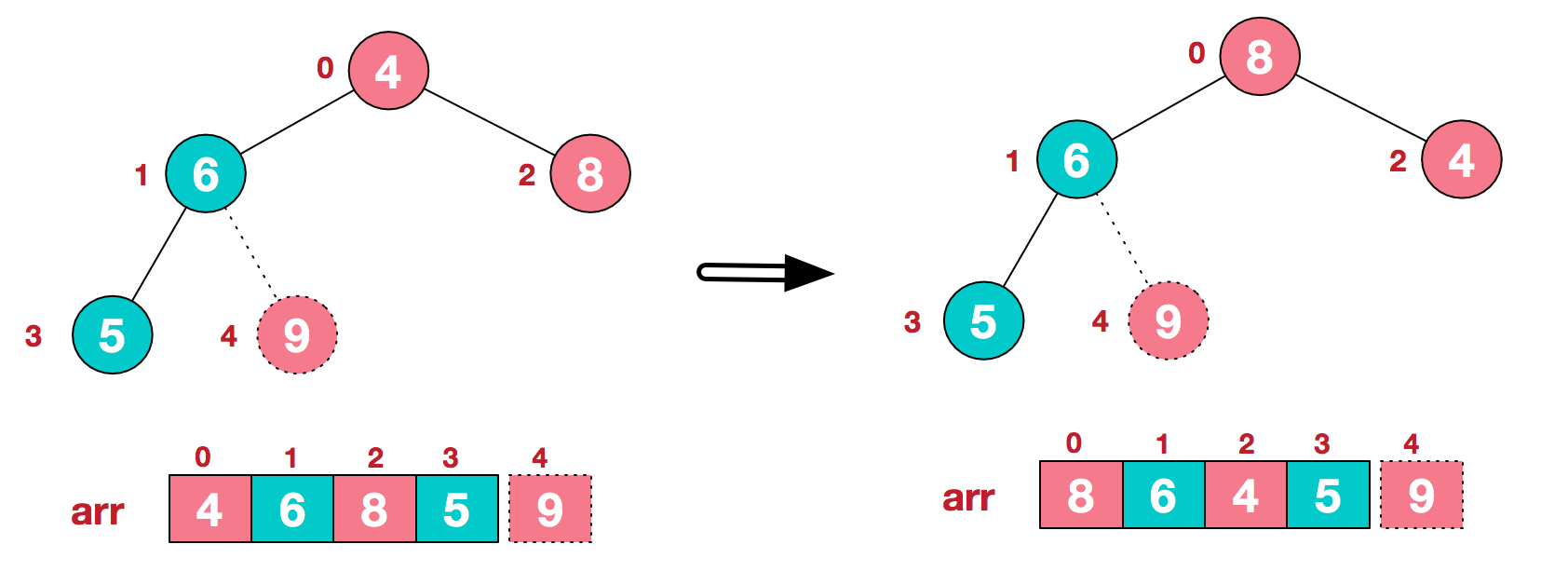
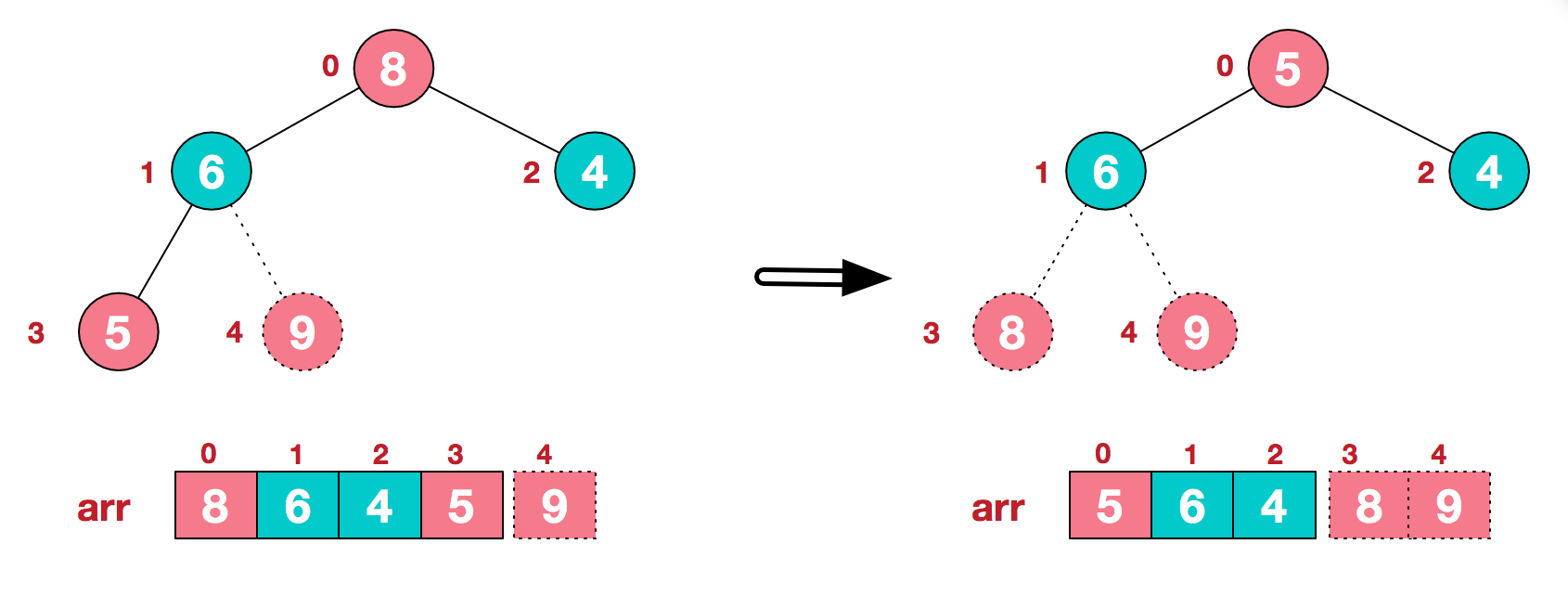
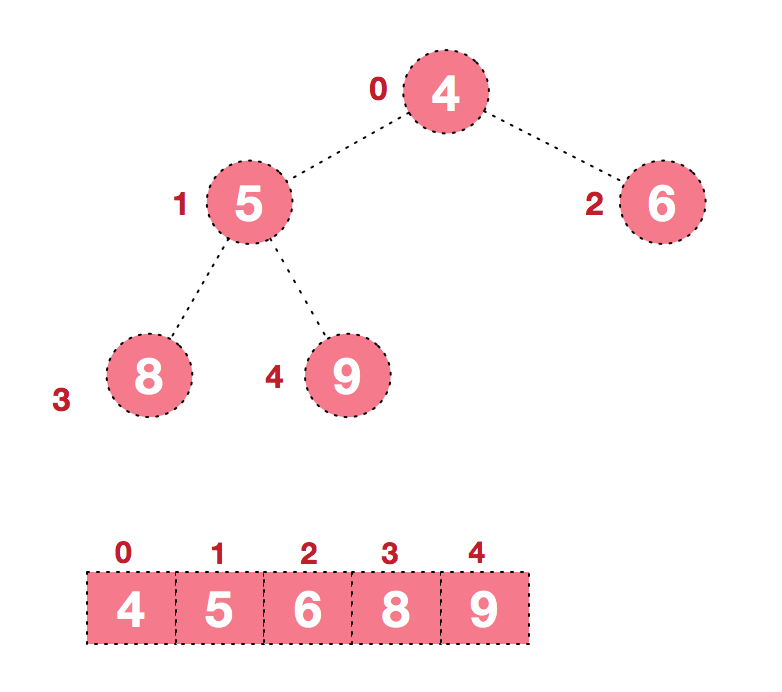
复杂度
时间$O(nlogn)$空间$O(1)$
稳定性
非稳定排序,原地排序
代码实现
ps:由于个人习惯,堆还是以1开始编号
这玩意整了很久,,,因为有点忘了
void sort_heap(int num[],int begin,int end)
{
//由于堆的节点编号与其性质息息相关,把需要排序的部分切出来做排序会比较合适()
int a[end-begin+1], i,cnt;
cnt = 0;
for (i = begin; i <= end;i++)
a[++cnt] = num[i];
void build_heap(int p,int len)
{
int ch;
ch = p;
for (ch = 2 * p; ch <= len;ch=2*p)
{
if(ch+1<=len && a[ch+1]>a[ch])
ch++;
if(a[ch]<=a[p])
break;
swap(&a[p], &a[ch]);
p = ch;
}
}
int p;
p = cnt / 2;
for (i = p; i >= 1;i--)
build_heap(i,cnt);
for (i = cnt; i >= 2; i--)
{
swap(&a[i], &a[1]);
build_heap(1, i - 1);
}
cnt = 0;
for (i = begin; i <= end;i++)
num[i] = a[++cnt];
}
于是所有比较型的排序都搞完了,接下来是计数型排序
计数排序
算法介绍
看完介绍,我:这算法也太tm暴力了吧。。。。就是开数组打标,看每个数出现的次数再把他全部排一遍。。。好家伙也太暴力了SOS
好家伙这玩意还不支持负数,太弱鸡了。。。
复杂度
时间$O(n+k) $空间$O(k) $ MLE警告阿SOS
稳定性
稳定排序,非原地排序
代码实现
弱智代码.jpg
void sort_count(int num[],int begin,int end)
{
int maxx,ans[end-begin+1],cnt,minn;
maxx = num[begin];
minn = (1<<30);
int i;
for (i = begin; i <= end;i++)
maxx = max(maxx, num[i]),minn=min(minn,num[i]);
int flag[maxx-minn+1];
for (i = 1; i <= maxx-minn+1;i++)
flag[i] = 0;
for (i = begin; i <= end; i++)
flag[num[i]-minn]++;
cnt = 0;
for (i = 1; i <= maxx-minn+1;i++)
if(flag[i]!=0)
{
int j;
for (j = 1; j <= flag[i];j++)
ans[++cnt] = i+minn;
}
cnt = 0;
for (i = begin; i <= end;i++)
num[i] = ans[++cnt];
}
桶排序
算法介绍
感觉是比较迷惑的算法,据说很快很牛逼,确实也挺牛的。但由于我不会链表,俺还是用 c++ vector来实现。。
是计数排序的高级版,总的来说就是把序列所有数据的区间分段,相当于分为多个桶,然后把数据一次按区间分别放到各个桶中,在每个桶中分别排序,最后将其合并就完了。
至于怎么查找区间内的所有数,来人,上二分!x
感觉很玄学不知道为啥这样就快很多了,据说数据越多越快x
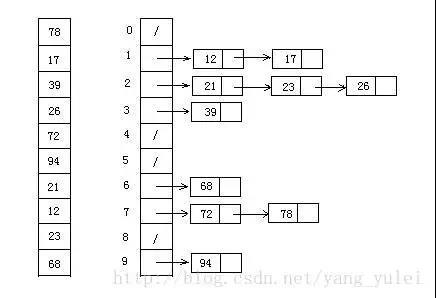
复杂度
时间$O(n+k) $最坏$O(n^2)$空间$O(n+k) $
稳定性
稳定排序,非原地排序
代码实现
注意奇怪的细节(
void sort_bucket(int num[],int begin,int end)
{
int len = end - begin + 1;
int maxx = -(1 << 30), minn = (1 << 30);
for (int i = begin; i <= end;i++)
{
maxx = max(maxx, num[i]);
minn = min(minn, num[i]);
}
int d = maxx - minn;
int bucket_cnt = d / 5 + 1;
vector<int> bucket[bucket_cnt+1];
int list[bucket_cnt];
for (int i = 1; i <= bucket_cnt;i++)
list[i] = minn + (i - 1) * 5;
for (int i = begin; i <= end; i++)
{
int loc = lower_bound(list + 1, list + 1 + bucket_cnt, num[i])-list-1;
if(loc==0)loc++;
bucket[loc].push_back(num[i]);
}
int cnt = begin;
for (int i = 1; i <= bucket_cnt;i++)
{
sort(bucket[i].begin(), bucket[i].end());
for (int j = 0; j < bucket[i].size();j++)
num[cnt++] = bucket[i][j];
}
}
基数排序
算法介绍
总的来说也是一种比较神奇的桶排,然后呢也比较鸡肋,只适合小范围的数据排序。
准备10个桶分别代表数字0-9,以个位数为第一个基准,将所有的数据按个位数字投进10个桶中,再按0-9的顺序将数据倒出来,接下来按十位,百位,依次类推,直到最高位,就挺好玩的x
由于c没有动态数组,还是用c++写

复杂度
时间$O(nk)$空间$O(n+k)$
稳定性
稳定排序,非原地排序(只要是计数类都是这样)
代码实现
void sort_radio(int num[],int begin,int end)
{
int maxx = 0;
for (int i = begin; i <= end;i++)
maxx = max(maxx, num[i]);
int cnt = 0,mod=10,dev=1;
while(maxx>0)
{
maxx /= 10;
cnt++;
}
vector<int> bucket[11];
for (int i = 1; i <= cnt;i++,dev*=10,mod*=10)
{
for (int j = begin; j <= end;j++)
{
int number = (num[j] % mod) / dev;
bucket[number].push_back(num[j]);
}
int coc = begin;
for (int j = 0; j <= 9;j++)
{
for (int k = 0; k < bucket[j].size();k++)
num[coc++] = bucket[j][k];
bucket[j].clear();
}
}
}
终于都写完啦撒花~~