信号与系统学习笔记

傅里叶变换Fourier Transform

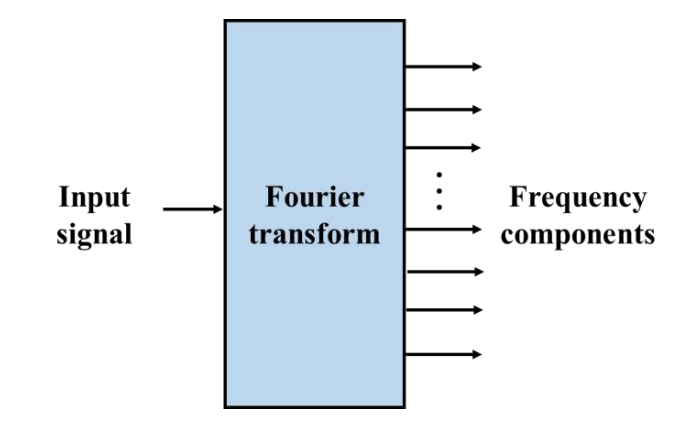
傅里叶变换主要应用于将信号经过处理后变成不同频率的组成

大概就会将合成的频率组合拆分成单个信号

有点类似于棱镜对于光，白光透过棱镜会分成不同的彩光。

将傅里叶变换看做棱镜，信号看做光来理解就差不多

首先是傅里叶级数

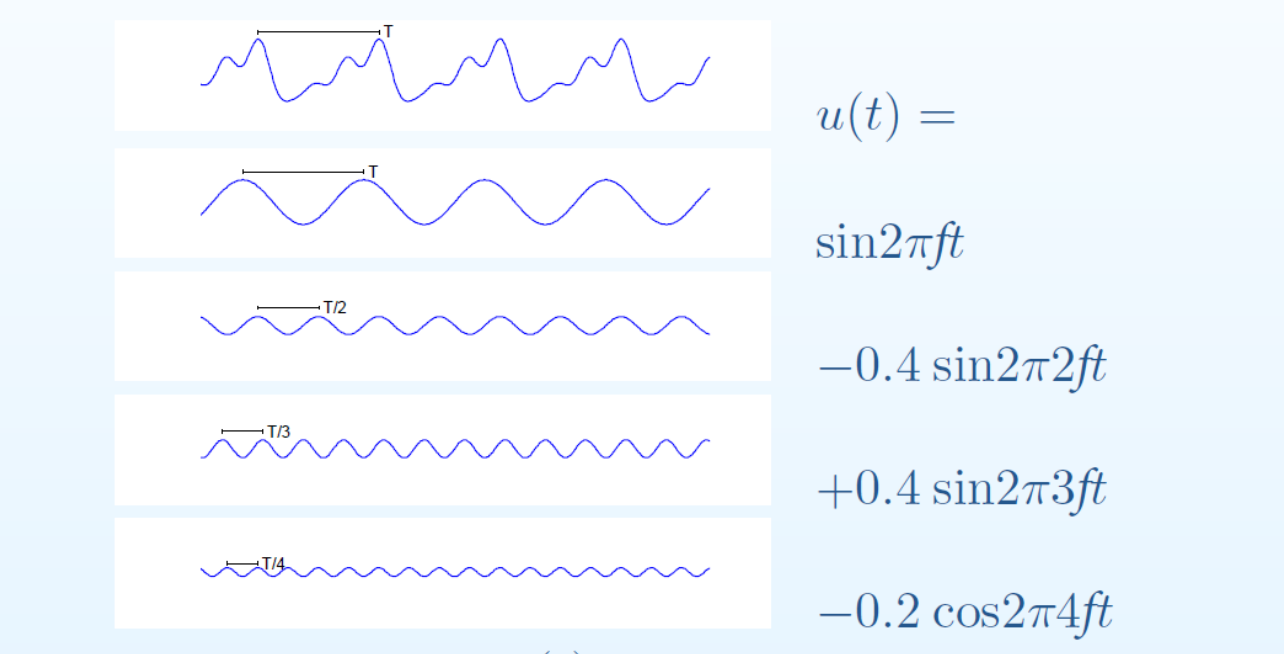
傅里叶级数的公式
$$
u(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos2\pi ft +b_n \sin 2\pi nft)
$$

$$
x(t) =\sum_{k=-\infty}^{\infty} a_{k}e^{jkw_{0}t}=\sum_{k=-\infty}^{\infty} a_{k}e^{jk\frac{2\pi}{T}t}
$$

$$
x[n] =\sum_{k \in \lt N \gt } a_{k}e^{jkw_{0}n}=\sum_{k \in \lt N \gt }a_{k}e^{jk\frac{2\pi}{T}n}
$$

$$
a_k =\sum_{n \in \lt N \gt} x[n]e^{-jkw_{0}n}=\sum_{x \in \lt N \gt}a_n e^{-jk\frac{2\pi}{T}n}
$$

主要把光分成红光