rt: 联赛复习 _ (: 3 | /) _ (以前已经做过的题就不再写了)
ps : 题目都是链接可点,部分简单题就不弄题意了,所有题目排列基本上按难度递增
注意,这里用的都是正解dp,不写任何暴力非正解混分做法
10k字纪念!!!
入门篇
难度评级 :普及- 至 普及+/提高
1. 总分 Score Inflation
难度评级 :普及-
裸的完全背包。
虽然是一道裸题,但通过回顾背包九讲对01背包有了更深刻的理解
之前一直没有想清楚01背包的一维是为什么要倒着推
二维式子是
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+val[i]);
这很好理解,但一维的就是
for(int i=1;i<=n;i++)
for(int j=V;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+val[i]);
为什么要倒着推?这是我以前一直没想清楚的。
很显然,我们需要啊保证$f[j]$这个状态一定是由$f[j-1]$ 转移过来的,如果我们是正着推,很显然$f[i][j]$有可能是$f[i ][j-w[i]]$也就是同层的推出来的,因为一个物品只能选一次,显然这就不对,只有倒着推,因为此时$f[i ][j-w[i]]$并没有状态,所以只能是$f[i -1][j-w[i]]$上一层的状态推出来的。
我终于想清楚了。_ (: 3 | /) _
对于完全背包就刚好相反,正着推就表示$f[i][j]$可以由$f[i ][j-w[i]]$推过来,也就正好是可以选多次!!刚好满足题意,于是完全背包的一维代码就是
for(int i=1;i<=n;i++)
for(int j=w[i];j<=V;j++)
f[j]=max(f[j],f[j-w[i]]+val[i]);
代码就不放了,毕竟很裸,只是借此写写心得
2. 精卫填海
难度评级 :普及-
变形的01背包,一开始把题目看错了。。。。
裸的跑一遍01背包,看最大值是否满足V,若不满足直接Impossible
满足从1-W跑一遍找最小的W满足$f[j]>=V$就直接输出就行
#include <bits/stdc++.h>
using namespace std;
const int N= 10000+110;
int n,m,f[N],V,W,w[N],val[N];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
V=read();n=read();W=read();
for(int i=1;i<=n;i++){val[i]=read();w[i]=read();}
for(int i=1;i<=n;i++)
for(int j=W;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+val[i]);
if(f[W]<V){printf("Impossible");return 0;}
for(int i=0;i<=W;i++)
if(f[i]>=V){printf("%d",W-i);break;}
return 0;
}
也比较水
3. 榨取kkksc03
难度评级 :普及/提高-
裸的二维费用背包
没有什么别的东西
#include <bits/stdc++.h>
using namespace std;
const int N=220;
int n,dp[N][N],M,T,m[N],t[N],maxx;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();M=read();T=read();
for(int i=1;i<=n;i++)t[i]=read(),m[i]=read();
for(int i=1;i<=n;i++)
{
for(int j=M;j>=m[i];j--)
for(int k=T;k>=t[i];k--)
dp[j][k]=max(dp[j][k],dp[j-m[i]][k-t[i]]+1);
}
for(int i=1;i<=M;i++)
for(int j=1;j<=T;j++)
maxx=max(maxx,dp[i][j]);
printf("%d",maxx);
return 0;
}
背包入门复习差不多到此为止
其实还有很多内容就日后有时间每个都码一个板子
4. Likecloud-吃、吃、吃
难度评级 :普及/提高-
题目简述
给一个长宽为$n,m$的点阵。一个点可以从自己的左前方,右前方或前方走过来,起点在最后一行的中间位置。求最大的答案。
题解
非常简单的二维路径设计dp,注意有一个小技巧是把走法翻转过来,起点变成终点;(我已开始竟没想到)
$$
dp[i][j]=max(max(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+mp[i][j];
$$
终点的答案是
$$
max(max(dp[n][pos],dp[n][pos-1]),dp[n][pos+1]);
$$
代码就非常基础
#include <bits/stdc++.h>
using namespace std;
const int N=220;
int n,m,dp[N][N],mp[N][N];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i][j]=read();
int pos=(m+1)/2;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
dp[i][j]=max(max(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+mp[i][j];
}
printf("%d",max(max(dp[n][pos],dp[n][pos-1]),dp[n][pos+1]));
return 0;
}
5. 最大正方形
难度评级 :普及/提高- 至 普及+/提高
题目简述
在一个$n*m$的只包含0和1的矩阵里找出一个不包含0的最大正方形,输出边长。
题解
设计状态$dp[i][j]$表示以$(i,j)$为右下角的最大正方形边长,也就是$mp[i][j]$必须为1。
一开始状态设计错了,就一直没想出转移方程。后来经过机房dalao的指导才发现错误,只有这样是可以转移的
我已开始以为是$dp[i][j]$表示$(1,1)到(i,j)$这整个方块的中最大正方形边长,发现这样是不可转移的。
其实是这个思想非常妙
if(!mp[i][j])dp[i][j]=0;
else dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1,maxx=max(maxx,dp[i][j]);
这样子转移就间接避免的判断是都组成正方形的过程,只有当这个点的左上周围三个点都能组成以x-1为边长的正方形时,这个点才能组成以x为边长的正方形
这个东西可以手推一下,反正非常巧妙
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,m,dp[N][N],mp[N][N],maxx;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i][j]=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(!mp[i][j])dp[i][j]=0;
else dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1,maxx=max(maxx,dp[i][j]);
}
printf("%d",maxx);
return 0;
}
基础篇
难度评级 :普及+/提高 至 提高+/省选-
1. 烹调方案
难度评级 :普及+/提高
题目简述
一共有$n$件食材,每件食材有三个属性,$a_i,b_i和c_i$,如果在t时刻完成第$i$样食材则得到$a_i-t*b_i$的美味指数,用第$i$件食材做饭要花去$c_i$的时间。
求美味度最大值
题解
说实话这一题还是比较有价值的,排序思路类似国王游戏,实则又是01背包变形。
一看题就觉得像是cxy 巨神出的codeforces ,但一交代码就发现不对,原来这一题的美味度可以减为负数。
于是就是先排序,再进行一波01背包就可以
类似国王游戏的排序
v是减少的速度(掉分速度),t是耗时
bool mmp(node x,node y)
{
return (x.v*x.t+y.v*(x.t+y.t))<(y.v*y.t+x.v*(x.t+y.t));
}
这个式子可以化简但是这样更清楚我就没化了
关于为什么局部最优就是全局最优使用一个单调函数来证明的,当时cxy 巨神讲过但是我不记得了QWQ,大概可以手推一下???反正和国王游戏差不多。。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+110;
int n,m;
ll ans,T,sumt,dp[N],maxx;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct node
{
ll v,t,val;
}a[N];
bool mmp(node x,node y)
{
return (x.v*x.t+y.v*(x.t+y.t))<(y.v*y.t+x.v*(x.t+y.t));
}
int main()
{
scanf("%lld%d",&T,&n);
for(int i=1;i<=n;i++)a[i].val=read();
for(int i=1;i<=n;i++)a[i].v=read();
for(int i=1;i<=n;i++)a[i].t=read();
sort(a+1,a+1+n,mmp);//保证这样的顺序最优
for(int i=1;i<=n;i++)
for(int j=T;j>=a[i].t;j--)
dp[j]=max(dp[j],dp[j-a[i].t]+a[i].val-j*a[i].v);
for(int i=1;i<=T;i++)maxx=max(maxx,dp[i]);
printf("%lld",maxx);
return 0;
}
2. 多米诺骨牌
难度评级 :提高+/省选-
题意简述
给你上下两个数列,数列上下可对应交换,求最小交换次数使上下数列之和的差值最小,即上面数列和为$S_1$,下面和为$S_2$,使$|S_1-S_2|$最小。
题解
显然是一个dp,然而我其实仍然没做出来。
我们可以把上下两个数列的差看做一个背包,于是就转化成立类似01背包的问题。
我们令$dp[i][j]$表示前$i$个数和为$j$的最小交换次数
因为j可能为负数,所以我们令maxn表示0,maxn-1表示-1,maxn+1表示1;
在忽略负数的情况下,我们可以得到状态转移方程
dp[i][j]=min(dp[i-1][j-val[i]],dp[i-1][j+val[i]]+1);
$val[i]$表示上下两个数列的差值(不加绝对值),j是枚举的背包容量,$dp[i-1][j-val[i]]$表示就是不翻转,
$dp[i-1][j+val[i]]+1$表示的就是上下翻转,$val[i]$的值反号,这都挺好理解的,和01背包写法很像。
最后统计答案的时候注意正负的答案同时取min,因为题意得差值是带绝对值的这一点要注意!
直接上代码,注意用了滚动数组优化
#include <bits/stdc++.h>
using namespace std;
const int N=1100;
int n,m,dp[3][N*2*5],val[N],minn=(1<<30);
//dp[i][j] 表示前i个数的和为j的最小翻转数
const int maxn=N*5;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
{
int x,y;
x=read();y=read();
val[i]=x-y;
}
for(int i=0;i<2;i++)
for(int j=-maxn;j<=maxn;j++)
dp[i][j+maxn]=(1<<30);
dp[0][maxn]=0;
for(int i=1;i<=n;i++)
{
for(int j=-maxn;j<=maxn;j++)
{
dp[i&1][j+maxn]=min(dp[(i-1)&1][j-val[i]+maxn],dp[(i-1)&1][j+val[i]+maxn]+1);
}
}
for(int i=0;i<=maxn;i++)
{
minn=min(dp[n&1][maxn+i],dp[n&1][maxn-i]);
if(minn!=(1<<30))
{
printf("%d",minn);
return 0;
}
}
return 0;
}
3. 创意吃鱼法
难度评级 :提高+/省选-
题目简述
给你一个$n*m$的矩阵,求最大的正方形边长满足在这个子正方形中只有其中一条对角线上全部是1,其余地方全部是0(可以左斜也可以右斜)。
题解
终于自己打出来一道题了!!! ( ╹▽╹ ) \ ( w ) /
这一道真真切切经历了16 —> 32 —> 72 —> 80 —> 100 的愉快过程
这一题解法很多,借鉴了最大正方形那题的思路,设计状态$dp[i][j]$表示以$(i,j)$为右下角或左下角的最大满足题意得正方形边长。至此大家都能想到暴力二维前缀和check的思路。
这里来介绍一下我的解题很捞的过程供大家自己找错和借鉴?
16分 :dp的时候只check了三个点,
受最大正方形的影响很深企图这样混分。。32分 :立马发现了自己漏洞的我就引进了二维前缀和,暴力check,但每次都只判了最大可能的边长,这为之后的二分操作奠定了基础
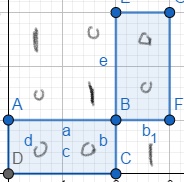
如上图,(从(3,3)点判断(2,2)这个点)判断这个子正方形就是judge蓝色阴影的部分的和是否为0,所以就是二维前缀和
72分 :一交发现嗯怎么分还是这么少???仔细读题一看发现对角线有两条所以有两种判断方式,于是写了两个judge又交了一遍,就愉快的72分
80分 : 发现一组hack数据一测WA掉了
4 4 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 1输出应该是3结果一测是2,马上发现了问题,原来在judge的时候只判断了最大可能的正方形却忽略的次小的正方形,就是在$dp[3][3]$这的地方应该是2却判成了1。想了很久没弄出解决办法就打了个暴力判断结合了我16分的代码,于是就涨了8分。。
100分 : 于是就有了二分,只要在每次judge时二分一个最大符合题意得最大边长就愉快的解决了!
有了以上的分析相信大家一看代码就懂了
#include <bits/stdc++.h>
using namespace std;
const int N=2520;
int n,m,dp[N][N],mp[N][N],maxx,sum[N][N],f[N][N];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int check(int x,int y,int len)
{
int nowx=sum[x][y-1]+sum[x-1][y-len-1]-sum[x][y-len-1]-sum[x-1][y-1];
int nowy=sum[x-1][y]+sum[x-len-1][y-1]-sum[x-1][y-1]-sum[x-len-1][y];
if(!nowx&&!nowy)
return 1;
else return 0;
}
int check2(int x,int y,int len)
{
int nowx=sum[x][y+len]+sum[x-1][y]-sum[x][y]-sum[x-1][y+len];
int nowy=sum[x-1][y]+sum[x-len-1][y-1]-sum[x-1][y-1]-sum[x-len-1][y];
if(!nowx&&!nowy)
return 1;
else return 0;
}
void two_point(int x,int y,int maxn)
{
int l=1,r=maxn;
while(l<=r)
{
int mid=(l+r)/2;
if(check(x,y,mid))l=mid+1;
else r=mid-1;
}
dp[x][y]=max(dp[x][y],(l+r)/2+1);
maxx=max(maxx,dp[x][y]);
}
void two_point2(int x,int y,int maxn)
{
int l=1,r=maxn;
while(l<=r)
{
int mid=(l+r)/2;
if(check2(x,y,mid))l=mid+1;
else r=mid-1;
}
dp[x][y]=max(dp[x][y],(l+r)/2+1);
maxx=max(maxx,dp[x][y]);
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i][j]=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sum[i][j]=mp[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(mp[i][j]==1)
{
two_point(i,j,dp[i-1][j-1]);
two_point2(i,j,dp[i-1][j+1]);
}
else dp[i][j]=0;
}
printf("%d",maxx);
return 0;
}
4. 垃圾陷阱
难度评级 :提高+/省选-
题目简述
一开始的体力是10,给出初始高度D,一共有N个垃圾,对于每个垃圾可以选择吃掉或堆放,同时每个垃圾还有固定的掉落时间。也就是每个垃圾有三个属性$T$表示垃圾掉落时间,$F$表示如果吃掉能增加的体力值,$H$表示堆放能堆起的高度,当然对于每个垃圾只能选择吃掉或堆放。
求在不死掉的情况下达到D的最早时间,若不能输出最长存活时间。(体力小于0则死亡)
题解
这一题也显然使一个变形的01背包,但我还是因为经验不足卡了很久。。
首先我们需要先按时间sort一遍,这很显然
我们令$dp[i][j]$表示前i个垃圾达到j高度的最长生命时间
转移方程为
if(dp[i-1][j]>=a[i].t)//若在此状态下还存活
dp[i][j]=max(dp[i-1][j]+a[i].val,dp[i][j]);//可以选择吃掉垃圾
if(dp[i-1][j-a[i].h]>=a[i].t&&j>=a[i].h)//还存活
dp[i][j]=max(dp[i-1][j-a[i].h],dp[i][j]);//或可以堆放
最后统计答案从头扫一遍,只要遇到$maxh>D$就直接退出输出,注意此时必须要求$dp[i][j]>=a[i].t$也就是此时还存活,这样更新$maxh$,然后每次找都更新$maxt$就行
代码如下
#include <bits/stdc++.h>
using namespace std;
const int N=1500;
const int INF=(1<<30);
int n,m,dp[N][N],T,t,maxh,maxt,pos,D;
struct node
{
int t,val,h;
bool operator < (const node &x)const
{
return t<x.t;
}
}a[N];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
D=read();n=read();T=10;
for(int i=1;i<=n;i++)
a[i].t=read(),a[i].val=read(),a[i].h=read();
sort(a+1,a+1+n);
dp[0][0]=T;//注意初始化
for(int i=1;i<=n;i++)
{
for(int j=0;j<=D;j++)
{
if(dp[i-1][j]>=a[i].t)
dp[i][j]=max(dp[i-1][j]+a[i].val,dp[i][j]);
if(dp[i-1][j-a[i].h]>=a[i].t&&j>=a[i].h)
dp[i][j]=max(dp[i-1][j-a[i].h],dp[i][j]);
}
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=D;j++)
{
if(dp[i][j]>=a[i].t)
maxh=max(maxh,j);
maxt=max(maxt,dp[i][j]);
}
if(maxh==D)
{
pos=i;break;
}
}
if(maxh==D)printf("%d",a[pos].t);
else printf("%d",maxt);
return 0;
}
5. 低价购买
难度评级 :普及+/提高- 至 提高+/省选-
题意简述
求一个序列的最长下降子序列及其最长长度的总方案数。
题解
这一题的第一问非常简单,是很基础的动规问题。这里为了方便就使用$O(n^2)$的普通算法。。。
实际是因为用O(log n)就并不会求方案数 第一问相信大家都会
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
if(a[i]<a[j])
f[i]=max(f[i],f[j]+1);
ans=max(ans,f[i]);
}
关键是第二问如何求方案数,这种问题我从来没有遇到过,,并没有想到还可以用另个一dp来求
用$t[i]$表示从1-i 的最长下降子序列的方案数 这个转移可以和f[i]一起转移
for(int j=1;j<i;j++)
{
if(f[i]==f[j]&&a[i]==a[j])t[j]=0;//如果这两个位置的数完全相同,最大的子序列长度也相同,就去重舍掉
else if(f[i]==f[j]+1&&a[i]<a[j])t[i]+=t[j];//如果满足f[i]是由f[j]转移过来,t[i]就加上t[j]的方案数
}
if(!t[i])t[i]=1;//如果没有表示他是最大的数,他自己就是一种方案
还是dp经验太少。。。
完整代码
#include <bits/stdc++.h>
using namespace std;
const int N=6000;
int n,m,a[N],f[N],ans,t[N],sum;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
if(a[i]<a[j])
f[i]=max(f[i],f[j]+1);
ans=max(ans,f[i]);
for(int j=1;j<i;j++)
{
if(f[i]==f[j]&&a[i]==a[j])t[j]=0;
else if(f[i]==f[j]+1&&a[i]<a[j])t[i]+=t[j];
}
if(!t[i])t[i]=1;
}
for(int i=1;i<=n;i++)if(f[i]==ans)sum+=t[i];
printf("%d %d",ans,sum);
return 0;
}
入土篇
难度评级 :提高+/省选- 至 省选/NOI-
ps:入土篇主要记录一些更加有思维难度的dp,如状压dp(主要是状压),此篇更新会更加缓慢,毕竟我真的不太会dp,现在开始学状压。。。。
我们先来熟悉一下状压dp的常用操作,偷来的图
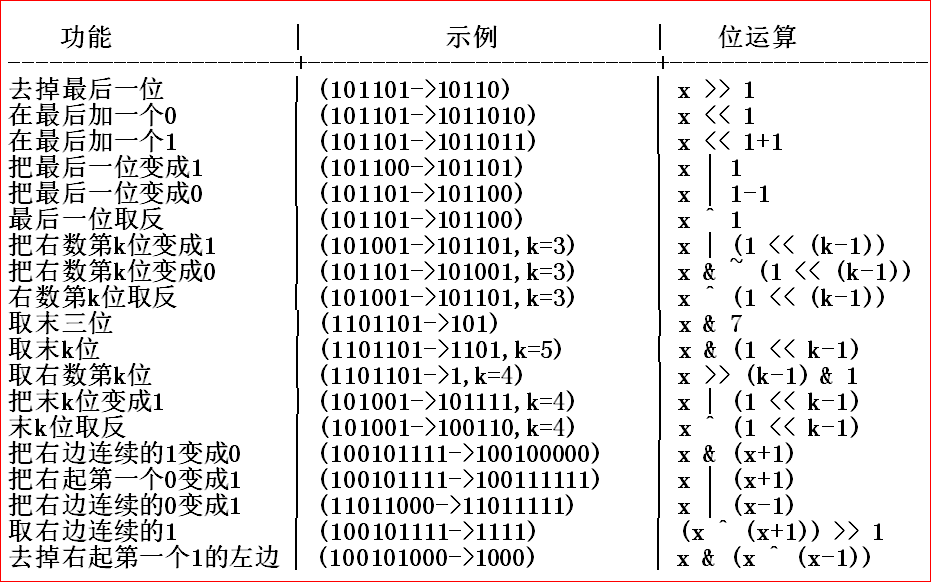
1. [USACO06NOV]玉米田Corn Fields
难度评级 :提高+/省选-
题意简述
输入玉米地的状态(用0 1表示),大小$n*m$( $ n,m<=12$),有的地方不能种(表示为0),要求同行不相邻,同列不相邻,有多少种种法 。
题解
状压dp入门题,非常好理解,很适合新手入门,基本看一下题解操作就能理解,可以说为初学者提供很好的练习途径。-\ ( v ) /-
首先我们定义几个数组
const int N=1 << 12+5;
const int M=13;
const int mod=1e9;
int f[M],g[N],dp[M][N],mp[M][M];
// f[i]表示每一行的状态 如011 -> 3
// dp[i][j]表示前i行的状态为j的合法方案数
// g[i]表示i状态是否合法 1表示合法
题目中首先要求同行不能有1是相邻的
g[i]=(!(i & (i << 1)) && !(i & (i >> 1)));
一个1的左右不能有相邻的1的意思是 i无论往右还是往左移一位and原来的数都是0就满足
我们可以举个栗子 101 右移1位 10 , 101 左移 1010 发现 &一下都是1
但 111 右移1位 11 左移 1110 (111 & 11) = 3 而 (111 & 1110)= 6 显然都不符合。这个东西手推一下大概还是很好理解的
接下来就是如何转移
for(int i=1;i<=n;i++)
{
for(int j=0;j<MAX;j++)
{
if((j & f[i])== j && g[j])//一是保证j状态合法,二是保证j状态没有在不该中的地方种植
//这个条件手模一下也很好理解
{
for(int k=0;k<MAX;k++)
{
if(!(k & j))//列与列之间没有1是相邻的
dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;//直接转移
}
}
}
}
答案统计就是加上所有$dp[n$][i]的答案
完整代码
#include <bits/stdc++.h>
using namespace std;
const int N=1 << 12+5;
const int M=13;
const int mod=1e9;
int n,m,MAX,ans;
int f[M],g[N],dp[M][N],mp[M][M];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i][j]=read(),f[i]=(f[i] << 1)+mp[i][j];
MAX=1 << m;
for(int i=0;i<MAX;i++)
g[i]=(!(i & (i << 1)) && !(i & (i >> 1)));
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<MAX;j++)
{
if((j & f[i])== j && g[j])
{
for(int k=0;k<MAX;k++)
{
if(!(k & j))
dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;
}
}
}
}
for(int i=0;i<MAX;i++)
ans=(ans+dp[n][i])%mod;
printf("%d",ans);
return 0;
}
2. [USACO08NOV]奶牛混合起来Mixed Up Cows
难度评级 :提高+/省选-
题目简述
给一串序列长度为$ n$,问你有多少种排列方式能使每个相邻两个数的差值大于$k$。
题解
很显然这也是一道状压dp入门题,但由于状压比较难所以就放到入土篇,像我就是特别的垃圾所以什么都不会。
首先我们需要一些基础知识
$ i \ and \ (1 << (k-1))==1$就是表示k存在于i这个状态中
$ i | (1 << (k-1))$就是往i这个状态中加入k这个状态,在二进制中| 就表示相加
这些的数学意义可以参考我一开始给出的表格
正式进入这一题。
我觉得这一题 的关键就是在设计状态上,像我这种蒟蒻就完全不知道应该如何设计。。。就想不到
设计$dp[i][j]$表示当目前状态为i的时候,这个序列以第j个数结尾
举个栗子:(编号) 421 这个序列的状态是 1011 十进制数为11 j 是 1
这个以j结尾千万不要搞错,是当前序列以j结尾不是整个最终的序列 。。 我就搞错了
所以转移方程就比较简单
当满足$i \ and \ (1 << (j-1))$ 表示此时j在i这个状态中,要不然i这个序列以j结尾就不合法
且$abs(a[j]-a[k])>m$ 符合题意
且$i|(1<<(k-1))≠i $ 此时k不在这个状态中
$dp[i|(1<< (k-1))][k]+=dp[i][j];$ 加入k这个状态后的i并转移
完整代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=(1 << 16);
const int M= 17;
ll dp[N][M],a[M],ans,MAX;
//dp[i][j] 在i状态时最后一个以j结尾
int n,m;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)dp[1 << (i-1)][i]=1;
MAX=(1 << n);
for(int i=0;i<MAX;i++)
for(int j=1;j<=n;j++)
if(i & (1 << (j-1)))
for(int k=1;k<=n;k++)
if(!(i & (1 << (k-1))) && abs(a[j]-a[k])>m)
dp[i|(1 << (k-1))][k]+=dp[i][j];
for(int i=1;i<=n;i++)
ans+=dp[MAX-1][i];
printf("%lld",ans);
return 0;
}
3. [SCOI2005]互不侵犯
难度评级 :提高+/省选-
题意简述
在$N×N$的棋盘里面放$K$个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
题解
历经前面两题的训练,这一题终于有了一定的思路,状态设计的也是对的,转移的大部分内容也可以由自己独立完成,只有一点点部分参考了一下题解。
因为有了国王数量的限制于是在与之非常类似的第一题的基础上增加了一维。
令$dp[i][j][k]$表示前i行,在j状态时,前i-1所拥有的总国王数为k
有了前面的基础,估计大家直接看代码也能直接懂我就直接放代码了。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=(1 << 9)+10;
const int M=10;
ll f[N],dp[M][N][9*9+6],n,m,g[N],MAX,num[N],ans;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int cal(int x)
{
int ans=0;
while(x)
{
if(x&1)ans++;
x= (x >> 1);
}
return ans;
}
void init()
{
for(int i=1;i<MAX;i++)
num[i]=cal(i);
}
int main()
{
n=read();m=read();
MAX=(1 << n);
init();//预处理每个状态对应的国王的数量
for(int i=0;i<MAX;i++)//注意先预处理第一行的情况
{
if(num[i]>m)continue;
dp[1][i][num[i]]=1;
}
for(int i=0;i<MAX;i++)
g[i]= (!(i & (i << 1)) && !(i & (i >> 1)));//处理出每个状态是否满足左右国王不相邻
for(int i=2;i<=n;i++)
{
for(int j=0;j<MAX;j++)//枚举这一层状态
{
if(!g[j])continue;
for(int k=0;k<MAX;k++)//枚举上一层状态
{
if((k&j)||((j >> 1)&k)||((j << 1)& k)||!g[k])continue;
//如果上下相邻,如果与右上方相邻,如果与左上方相邻 都要舍去
for(int h=0;h<=m;h++)//枚举前i-1层可以有多少个国王
{
if(h+num[j]>m)continue;//如果已经大于kcontinue
dp[i][j][h+num[j]]+=dp[i-1][k][h];//直接由i-1行的状态转移过来
//num[j]是当前第i行的国王数,所以前i行就是h+num[j]个国王
}
}
}
}
for(int i=0;i<MAX;i++)//直接统计每种状态的答案
ans+=dp[n][i][m];
printf("%lld",ans);
return 0;
}
4. [NOI2001]炮兵阵地
难度评级 :提高+/省选- 至 省选/NOI- 这人认为这一题还是比较难写的,对于我这个入门选手来说
题意简述
给定$n*m$($n<=100,m<=10)$的一张图,$P$能放炮兵,$H$表示不能放炮兵。一个炮兵的攻击范围如下图,问最多能放多少个炮兵。
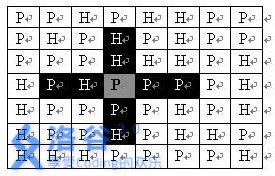
题解
不得不说这道题相比前面几道还是难度加大了的一些,思想很裸,但是代码还是要细心码
因为这一题设计到两行的状态
于是我们要设计三维$dp[i][j][k]$表示前i行,这一排为j状态,上行为k状态的最多放置炮兵数量
因为n比较大,为了防止MLE就要滚一下,这一行状态之和上一行有关就可以瞎jb滚一波
主要状转方程
$$
dp[i\&1][j][k]=max(dp[i\&1][j][k],dp[(i-1)\&1][k][h]+num[j]);
$$
还是和上题一样直接看代码讲解。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N= (1 << 10)+5;
const int M=110;
int n,m,cnt;
ll dp[2][N][N],mp[M],MAX,num[N],s[N],ans,Mp[M][11];
// dp[i][j][k] 1-i行这一排为j状态,上行为k状态的最多放置炮兵数量
char ch[M];
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int cal(int x)
{
int ans=0;
while(x)
{
if(x&1)ans++;
x =(x >> 1);
}
return ans;
}
void init()
{
for(int i=0;i<MAX;i++)
if((!(i & (i << 1))) && (!(i & (i << 2))) && (!(i & (i >> 1))) && (!(i & (i >> 2))))//初始化判断。要求左右两格都不能放炮兵
{
++cnt;
s[cnt]=i;
num[cnt]=cal(i);
if((i & mp[1])==i)dp[1][cnt][0]=num[cnt];//顺便把第一行的状态初始化
}
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
{
scanf("%s",ch);
for(int j=0;j<m;j++)
if(ch[j]=='P')Mp[i][j+1]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mp[i]=(mp[i] << 1)+Mp[i][j];//我这个是模仿例1弄的判断方式,详见例1
MAX= 1 << m;
init();
//初始化第二行,因为要从第三行开始转移
for(int i=1;i<=cnt;i++)
for(int j=1;j<=cnt;j++)
if(((s[i] & mp[1])==s[i]) && ((s[j] & mp[2])==s[j]) && !(s[i] & s[j]) )
//判断i,j状态不与原图矛盾,i,j上下没公共边,实际上第一个判断不写也没有影响
dp[0][j][i]= max(dp[1][i][0]+num[j],dp[0][j][i]);
for(int i=3;i<=n;i++)
{
for(int j=1;j<=cnt;j++)//第i层状态
{
if((s[j] & mp[i])!=s[j])continue;//j不和原图矛盾
for(int k=1;k<=cnt;k++)//枚举第i-1层状态
{
if((s[k] & mp[i-1])!=s[k]||(s[j] & s[k]))continue;//j不矛盾且k,j没公共边
for(int h=1;h<=cnt;h++)//枚举第i-2行状态
{
if(((s[h] & mp[i-2])!= s[h] )||(s[h] & s[j])|| (s[h] & s[k]))continue;//这个与上面的条件相同
dp[i&1][j][k]=max(dp[i&1][j][k],dp[(i-1)&1][k][h]+num[j]);
//i从i-1的状态转移过来,注意不要写反
}
}
}
}
for(int i=1;i<=cnt;i++)
for(int j=1;j<=cnt;j++)
ans=max(ans,dp[n&1][i][j]);
printf("%lld",ans);
return 0;
}
大概就这么多,代码细节要非常注意,不要因为脑子混就写反写错。
5. 宝藏
难度评级: 省选/NOI-
题目简述
请选择合适的方案,满足已经属于同一个联通块中的两点间不会有直接相连的第二条边,
同时给定两点间连边的代价,为 $L \times K $
试求在花费最少代价的情况下使得最终所有节点在同一个联通块中
( $L \times K $ 为起点到当前点的所经过的节点数乘当前边长度)
题解
经典的NOIP2017Day2T2,这道题之所以经典也是因为这道题做法很多
我这次又重新写了一个状压,之前抄了一个玄学搜索+剪枝,还有一种玄学的模拟退火。
然而我写的是错的状压,很多题解都是这个做法,于是重新膜了一篇正解
AC记录对比 (加O2)
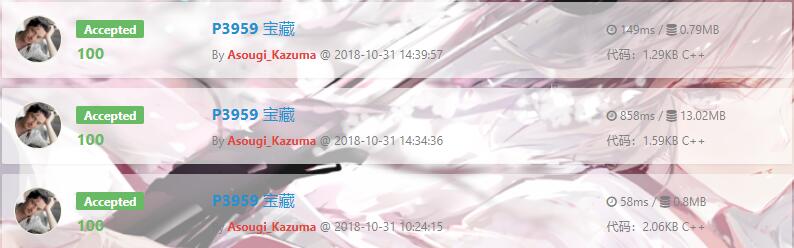
第一个为随机算法 综合排名第二,但是不保证正确性
第二个是正解状压,很慢很大空间但是正解
第三个是玄学搜索+剪枝 就非常的强,综合排名第一,可是我永远学不来
· 随机化算法(非模拟退火)
这个也参考了机房 dalao 的思路,感觉非常神奇
说来你可能不信这是目前第二快的算法。
算法是每次随机一个挖宝藏的顺序,并找到在这个顺序下挖宝藏的最小代价。
不断更新,若这个顺序不成立直接退出
直接看代码,简单易懂。。。
#include <bits/stdc++.h>
using namespace std;
const int N=13;
const int INF=1061109567;
int n,m,dis[N][N],a[N],road[N],ANS=INF;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
srand(time(NULL));
int t=clock();
n=read();m=read();
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=m;i++)
{
int x,y,z;
x=read();y=read();z=read();
dis[x][y]=dis[y][x]=min(z,dis[x][y]);
}
for(int i=1;i<=n;i++)a[i]=i;
for(int i=1;i<=7000;i++)
{
if(clock()-t>=950000)break;
random_shuffle(a+1,a+1+n);
memset(road,0,sizeof(road));
road[a[1]]=1;
int ans=0;
for(int j=2;j<=n;j++)
{
int sum=INF;
for(int k=1;k<j;k++)
{
if(dis[a[j]][a[k]]!=INF&&dis[a[j]][a[k]]*road[a[k]]<sum)
{
sum=dis[a[j]][a[k]]*road[a[k]];
road[a[j]]=road[a[k]]+1;
}
}
if(sum==INF){ans=INF;break;}
else ans+=sum;
}
ANS=min(ans,ANS);
}
printf("%d",ANS);
return 0;
}
· 状压dp(正解)
膜了一下rqy神仙的正解,之前写的是错的就非常难受,赶紧补了一篇正解虽然我不是非常理解
设计$dp[i][j][s]$bi表示从起点到节点j的距离为i,要从j开始挖边,挖通集合S的最小代价。
在转移的时候直接枚举从j出发的第一条边j—>k,再进一步枚举从k开始打通的自集$S2 \subset S$
于是状转方程
$$
f_{i,j,S}=min(dis[j][k]*(i+1)+f_{i+1,k,S_2-{k}}+f_{i,j,S-S_2} \ \ (k \in S_2 \in S,j \not\in S)
$$
最后统计答案$f_{0,i,U-{i}}$,$U$表示全集。
$nt[i]$表示每个集合的最小元素,预处理,先枚举$S_2$用来减少枚举时间。
有关位运算的知识
像 $S \ \&$ ~ $S_2$就相当于在集合$S$中去掉$S_2$
可以说在位运算中 & ~就相当于减号,|就相当于加号,这样理解写代码和看代码就会清晰很多
具体对方程的解释请看代码
#include <bits/stdc++.h>
using namespace std;
const int N=14;
const int INF=1061109567;
int n, m,dis[N][N],road[N],ans=INF,f[N][N][1 << N],siz[1 << N],nt[1 << N],MAX;
//dp[i][j][s] 表示从起点到节点j的距离为i,要从j开始挖边,挖通集合S的最小代价。
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main()
{
n=read();m=read();
memset(f,0x3f,sizeof(f));
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=m;i++)
{
int x,y,z;
x=read();y=read();z=read();
x--;y--;
dis[x][y]=dis[y][x]=min(dis[x][y],z);
}
MAX=1 << n;
for(int i=1;i<MAX;i++)siz[i]=siz[i & (i-1)]+1;//i中有多少个1,即已经有了多少个点
for(int i=0;i<n;i++)nt[1 << i]=i;
for(int i=1;i<MAX;i++)nt[i]=nt[i & -i];//预处理每个集合的最小元素,是类似树状数组的lowbit
for(int i=0;i<n;i++)f[n-1][i][0]=0;
for(int j=n-2;~j;j--)//j代表起点到i的距离,经过了多少条边
for(int i=0;i<n;i++)
{
f[j][i][0]=0;
for(int S=1;S<MAX;S++)
if(!((1 << i)& S) && (siz[S]<=n-j-1))//保证经过的总点数不大于n,i不属于S
for(int S2=S;S2;S2=(S2-1) & S)//S2不断递减,且S2属于S集合
if(f[j][i][S & ~S2]<f[j][i][S])//出现了更优的答案进一步更新
{
int tmp=S2;
for(int k=nt[tmp];tmp;k=nt[tmp &= ~(1 << k)])//像当与不断在tmp中去掉第k位,也就是枚举从j能到达那些点
if(dis[i][k]!=INF)
f[j][i][S]=min(f[j][i][S],
(j+1)*dis[i][k]+f[j+1][k][S2 & ~(1 << k)]+f[j][i][S & ~S2]);
//先是加上开拓j-k这条路的花费,再加上从k开始向后拓展S2不包括k的部分的花费,以及从i要开始拓展S去掉S2的部分的总花费,总是是把S拆开再把S2拆出一个点k的思路来转移
}
}
for(int i=0;i<n;i++)ans=min(ans,f[0][i][(MAX-1) & ~(1 << i)]);
printf("%d",ans);
return 0;
}
· 玄学搜索+剪枝
因为我并不是很会就不仔细写了,总之大家看看就行
#include <bits/stdc++.h>
#define ll long long
#define INF (1<<30)
using namespace std;
const int N=1000+110;
int n,m,cnt,vis[N];
int tmp,dis[20][20];
int lev[20], d[20];
//lev[i] 表示点距离初始点的距离
//d[i]表示出度
int tar[20][20];
//tar[i]表示存下每个点能到的点
int ans = INF, tot,p;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void dfs(int num,int x)
{
for(int i=num;i<=cnt;i++)
{
if(tot+tmp*lev[vis[i]]>=ans)return ;
for(int j=x;j<=d[vis[i]];j++)
{
if(!lev[tar[vis[i]][j]])
{
cnt++;
vis[cnt]=tar[vis[i]][j];
tmp-=dis[vis[cnt]][tar[vis[cnt]][1]];
tot+=dis[vis[i]][vis[cnt]]*lev[vis[i]];
lev[vis[cnt]]=lev[vis[i]]+1;
dfs(i,j+1);
tot-=dis[vis[i]][vis[cnt]]*lev[vis[i]];
lev[vis[cnt]]=0;
tmp+=dis[vis[cnt]][tar[vis[cnt]][1]];
cnt--;
}
}
x=1;
}
if(cnt==n)
{
ans=min(ans,tot);
return ;
}
}
bool mmp(int a,int b)
{
return dis[p][a]<dis[p][b];
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=(1<<30);
for(int i=1;i<=m;i++)
{
int x,y,w;
x=read();y=read();w=read();
if(dis[x][y]<w)continue;
if(dis[x][y]==INF)
tar[x][++d[x]]=y,tar[y][++d[y]]=x;
dis[y][x]=dis[x][y]=w;
}
for(int i=1;i<=n;i++)
{
p=i;
sort(tar[i]+1,tar[i]+1+d[i],mmp);
tmp+=dis[i][tar[i][1]];
}
for(int i=1;i<=n;i++)
{
tot=0;cnt=1;//目前搜到的点数
vis[1]=i;//第一个访问
tmp-=dis[i][tar[i][1]];
lev[i]=1;
dfs(1,1);
lev[i]=0;
tmp+=dis[i][tar[i][1]];
}
printf("%d",ans);
return 0;
}
这个dp系列到此就差不多结束了!!
完结散花★,° :.☆( ̄▽ ̄)/ : .°★ 。
总的来说都不是非常难的题目,大多数都是蓝题,其他的dp题就开另一个坑来写吧~~
每个篇章5题就非常整齐