今天又来学习神仙算法!
曰:神奇的
Kruskal 重构树
- 什么是重构树
其实就是在进行kruskal操作时,就重新构造一个新的树让这个树有一些神奇的性质把
边权改为点权,于是就有了2*n-1的新的节点
- 性质
1.这是一个二叉树
2.原树与新树两点间路径上边权(点权)值相等
3.子节点的边权小于等于父亲节点
4.原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权
- 构造过程
在进行Kruskal的过程中,每次找到一个最短的边,若此时这两个点不在一个集合中,就把这两个点加入一个集合。
并把他们分别向另一个新建的节点连边,新节点作为父亲节点
并把此时的边权赋给此时的新节点。不断重复这个操作就形成了
一棵Kruskal 重构树
看了这些也许还有些不理解,那就拿一个例题来看看就十分好懂了!
根据原图我们建图是这样
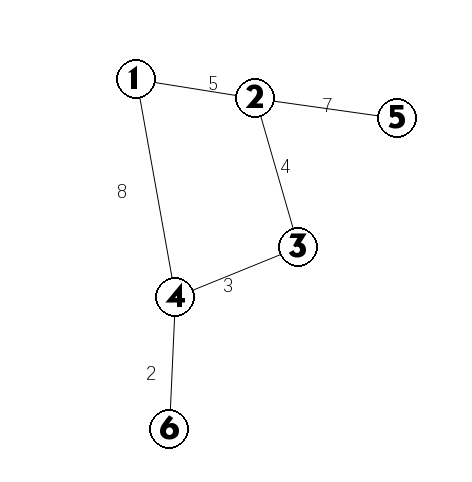
然后我们构建的Kruskal重构树是这样的
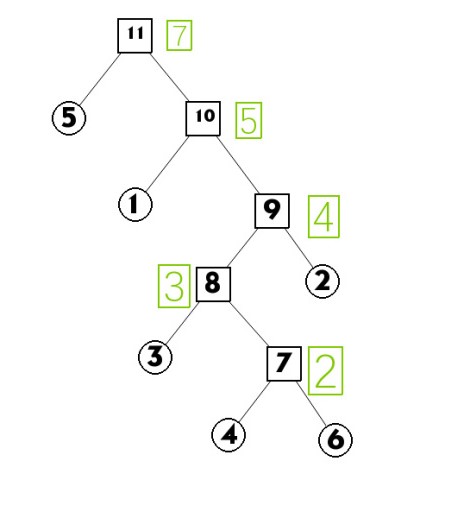
具体的建树过程如下:
- 按边权从小到大排序
- 当前的最小边是4 6 2,发现此时4,6不在一个集合中,新建节点7,并把4,6向7连边,把7的权值赋为2,将4,6加入7的集合中。
- 当前最小的边为3 4 3,此时3,4仍不在在一个集合中,新建节点8,并把3,7向8连边,把8的权值赋为3,并将3,7加入8的集合中。
- 当前最小的边为2 3 4,此时3,2仍不在在一个集合中,新建节点9,并把8,2向9连边,把9的权值赋为4,并将2,8加入9的集合中。
- 当前最小的边为1 2 5,此时1,2仍不在在一个集合中,新建节点10,并把9,1向10连边,把10的权值赋为5,并将1,9加入10的集合中。
- 当前最小的边为2 5 7,此时5,2仍不在在一个集合中,新建节点11,并把10,5向11连边,把11的权值赋为7,并将10,5加入11的集合中。
- 当前最小的边为1 4 8,发现1,4已经在一个集合里,故跳过。
- 最后,建树完成!
代码
代码就比较好搞了,树剖求lca,一看代码就懂。
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define il inline
using namespace std;
const int N=3e4+110;
int n,m,head[N],cnt,fa[2*N],pos[N],w[N],sizee[N],deep[N],q,tot,top[N],son[N];
il int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct node
{
int to,nt;
}edge[N*2];
struct edg
{
int u,v,w;
}e[N];
bool mmp(edg a,edg b)
{
return a.w<b.w;
}
void add(int x,int y)
{
++cnt;
edge[cnt].nt=head[x];
edge[cnt].to=y;
head[x]=cnt;
++cnt;
edge[cnt].nt=head[y];
edge[cnt].to=x;
head[y]=cnt;
}
int findf(int x)
{
if(x==fa[x])return x;
else return fa[x]=findf(fa[x]);
}
void Kruskal_build()
{
tot=n;
for(int i=1;i<=m;i++)
{
int fx=findf(e[i].u);
int fy=findf(e[i].v);
if(fx==fy)continue;
tot++;
add(tot,fx);
add(tot,fy);
fa[fx]=tot,fa[fy]=tot;
w[tot]=e[i].w;
}
}
void dfs(int x,int fa1,int d)
{
deep[x]=d;fa[x]=fa1;sizee[x]=1;
for(int i=head[x];i;i=edge[i].nt)
{
int v=edge[i].to;
if(v==fa1)continue;
dfs(v,x,d+1);
sizee[x]+=sizee[v];
if(sizee[v]>sizee[son[x]])son[x]=v;
}
}
void dfs2(int x,int tp)
{
top[x]=tp;
if(!son[x])return;
dfs2(son[x],tp);
for(int i=head[x];i;i=edge[i].nt)
{
int v=edge[i].to;
if(v!=son[x]&&v!=fa[x])
dfs2(v,v);
}
}
int lca(int a,int b)
{
while(top[a]!=top[b])
{
if(deep[top[a]]>deep[top[b]])
a=fa[top[a]];
else b=fa[top[b]];
}
if(deep[a]>deep[b])return b;
else return a;
}
int main()
{
n=read();m=read();q=read();
for(int i=1;i<=n;i++)
fa[i]=i,fa[i+n]=i+n;
for(int i=1;i<=m;i++)
e[i].u=read(),e[i].v=read(),e[i].w=read();
sort(e+1,e+1+m,mmp);
Kruskal_build();
int rt=findf(1);
memset(fa,0,sizeof(fa));
dfs(rt,0,rt);
dfs2(rt,rt);
for(int i=1;i<=q;i++)
{
int x,y;
x=read();y=read();
printf("%d\n",w[lca(x,y)]);
}
return 0;
}